#C = (\frac{1}{C_1} + \cdots + \frac{1}{C_n})^{-1} # and in parallel is # C = C_1 + \cdots + C_n# Capacitance?
1 Answer
I'm not sure exactly what is being asked here, but you are correct in how capacitance is calculated for connection in series and in parallel.
When connected in series, the total capacitance is less than the capacitance of any one capacitor in the connection.
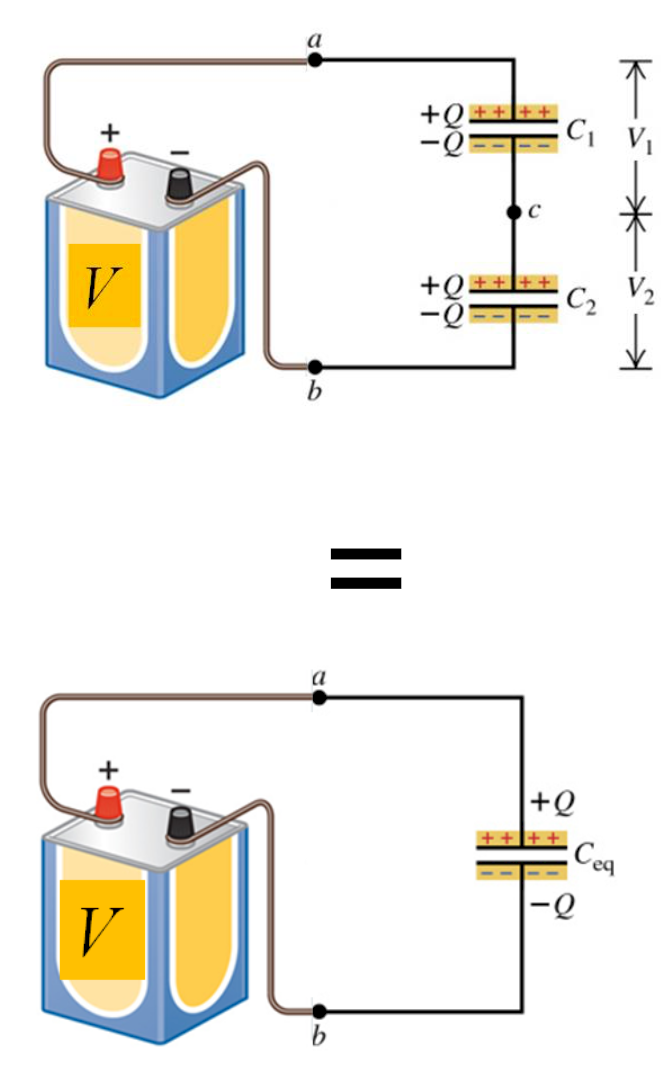
The equation for the total (or equivalent) capacitance of a set of capacitors connected in series follows the same form of the equation for resistors connected in parallel.
#C_"total"=(1/C_1+1/C_2+...+1/C_n)^(-1)#
For capacitors connected in parallel, the total capacitance is found by simply adding the capacitance of each individual capacitor which contributes. Therefore, the total capacitance for this situation is more than the capacitance of any individual capacitor.
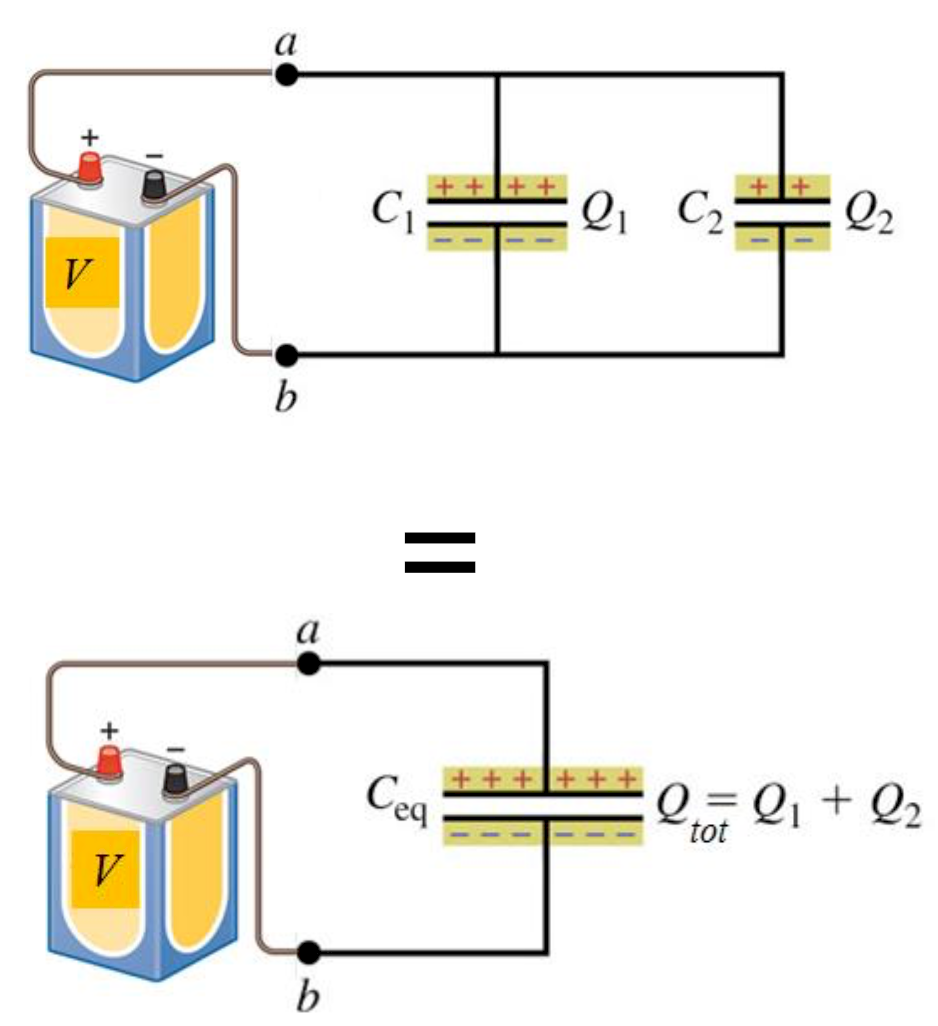
The equation for the total capacitance for capacitors connected in parallel follows the same form of the equation for resistors connected in series.
#C_"total"=C_1+C_2+...+C_n#

