The coordinates of the centroid of a triangle are the arithmetic mean of the x and y coordinates of the vertices. How do you prove this?

2 Answers
Somebody N.
Jun 14, 2018

See below.

Explanation:

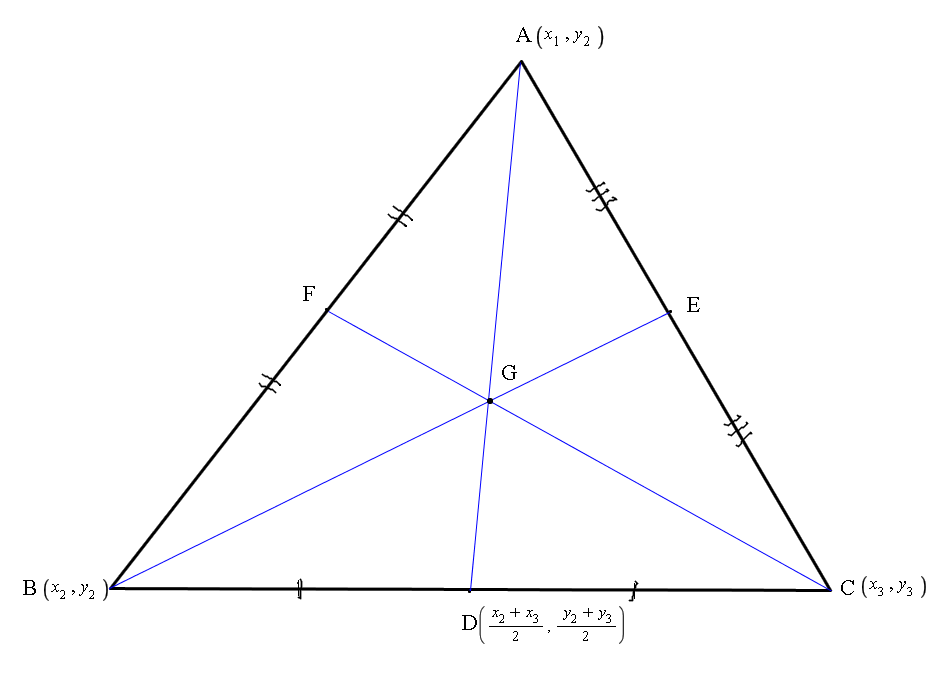
enter image source here

The centroid #G# lies #2/3# along the median from each vertex #A, B, C#

Looking at the median #AD#

The co-ordinates of #D# can be found using the midpoint formula:

#D=((x_2+x_3)/2,(y_2+y_3)/2)#

The point #G# divides #AD# in the ratio #2:1#

The co-ordinates of #G# are calculated using the section formula:

The Section Formula

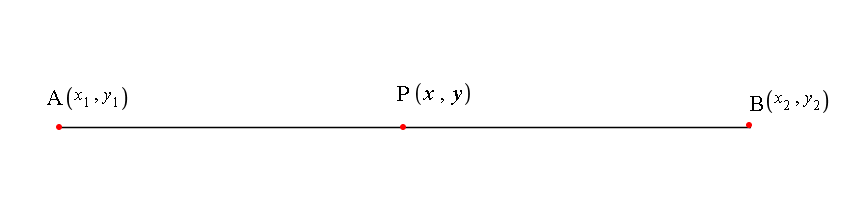
enter image source here

The point #P# lies on the line #AB#, such that:

#AP:PB=m:n#

#P " is " m/(m+n)xxAB# away from #A#

For #x#:

#x=x_1+m/(m+n)xx(x_2-x_1)#

# \ \ \ =x_1+(mx_2)/(m+n)-(mx_1)/(m+n)#

# \ \ \ \=((m+n)x_1+mx_2-mx_1)/(m+n)#

# \ \ \ \=(mx_2+nx_1)/(m+n)#

For #y#:

#y=y_1+m/(m+n)xx(y_2-y_1)#

# \ \ \ =y_1+(my_2)/(m+n)-(my_1)/(m+n)#

# \ \ \ \=((m+n)y_1+my_2-my_1)/(m+n)#

# \ \ \ \=(my_2+ny_1)/(m+n)#

#:.#

#P=((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n))#

Now back to the beginning:

Our ratio is #m:n=2:1#

We are using median #AD#

Using section formula for #bbx# co-ordinate.

#x=(2((x_2+x_3)/2)+x_1)/(2+1)color(white)(88)# ( note# (x_2+x_3)/2# is point D )

#x=(x_1+x_2+x_3)/3#

Using section formula for #bby# co-ordinate.

#y=(2((y_2+y_3)/2)+y_1)/(2+1)#

#y=(y_1+y_2+y_3)/3#

So co-ordinates of the centroid are:

#G=((x_1+x_2+x_3)/3,(y_1+y_2+y_3)/3)#

Note:

To find this we used the fact that the centroid divided the median in the ratio #2:1#. The proof of this wasn't included, but this can be verified by the use of vectors and the fact that the six triangles formed by the medians inside the triangle #ABC# all have the same area.

This is from the mentioned text book. As you can see it isn't a rigorous proof like the one in the other answer, but maybe it will be of some help to you.

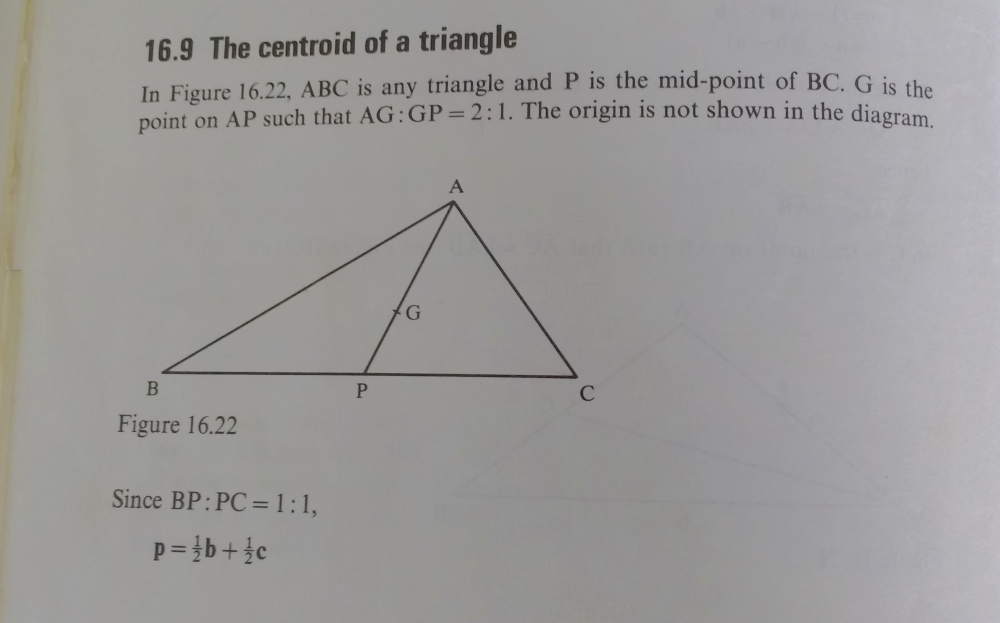
enter image source here

enter image source here

Dean R.
Jun 15, 2018

Triangle ACE, Vertices #A(a,b), C(c,d), E(e,f)#

Midpoints of the sides

#B={A+C}/2=({a+c}/2, {b+d}/2)#

#D={A+E}/2=({a+e}/2, {b+f}/2)#

#F={C+E}/2=({c+e}/2, {d+f}/2)#

We'll do the medians parametrically so we can show the centroid divides the median into segments ratio #2:1#.

Parametric equations for the medians

From #E# to #B={A+C}/2#

# EB= (1-t)E+tB = E + t({A+C}/2 - E) = E + t/2(A+C-2E)#

From #A# to #D={C+E}/2#

# AD= A + u({C+E}/2 - A) = A + u/2(C+E-2A)#

These meet at #G# which we want to show is the centroid:

#G = E + t/2(A+C-2E) = A + u/2(C+E-2A)#

# e + t/2(a+c-2e) = a +u/2(c+e-2a)#

#f + t/2(b+d-2f) = b+ u/2(d+f-2b)#

# t(d+f-2b)(a+c-2e) = 2(d+f-2b)(a-e)+u(d+f-2b)(c+e-2a)#

# t(c+e-2a)(b+d-2f) = 2(c+e-2a)(b-f)+ u(c+e-2a)(d+f-2b)#

#t ( (d+f-2b)(a+c-2e)- (c+e-2a)(b+d-2f)) = 2(d+f-2b)(a-e) - 2(c+e-2a)(b-f) #

Getting messy.

#t = ( 2(d+f-2b)(a-e) - 2(c+e-2a)(b-f) ) / ( (d+f-2b)(a+c-2e)- (c+e-2a)(b+d-2f))#

#t = { 2 ( ( ad + af -2ab -de -ef +2be)-(bc+be-2ab-cf-ef+2af ) ) }/{ ( ad+af-2ab +cd +cf-2bc -2de -2ef +4be ) - ( bc+be-2ab +cd+de-2ad -2fc-2ef+4af ) } #

#t = { 2 ( ad -de + be-bc+cf -af ) }/{ ( 3ad-3af +3cf-3bc -3de +3be ) } #

#t = 2/3 #

Recall #G = E + t(B-E) = t/2(A+C-2E)#

#t=2/3# shows #G# divides the median #EB# into a 2:1 ratio, #EG=2BG.#

#G = E + t/2(A+C-2E) = E+((2/3)/2)(A+C-2E)= E+1/3(A+C-2E)=1/3(A+C+E)#

That shows #G# is the average of the respective coordinates.

Since we'll get the same #2/3# starting from the other vertices, we'll get the same point #G#, i.e. we've shown the medians are concurrent, they meet at a single point, so we're justified in calling #G# the centroid.

Related questions
Impact of this question
4253 views around the world
You can reuse this answer
Creative Commons License