Question

How to find the point of intersection for all values of m,c and a?

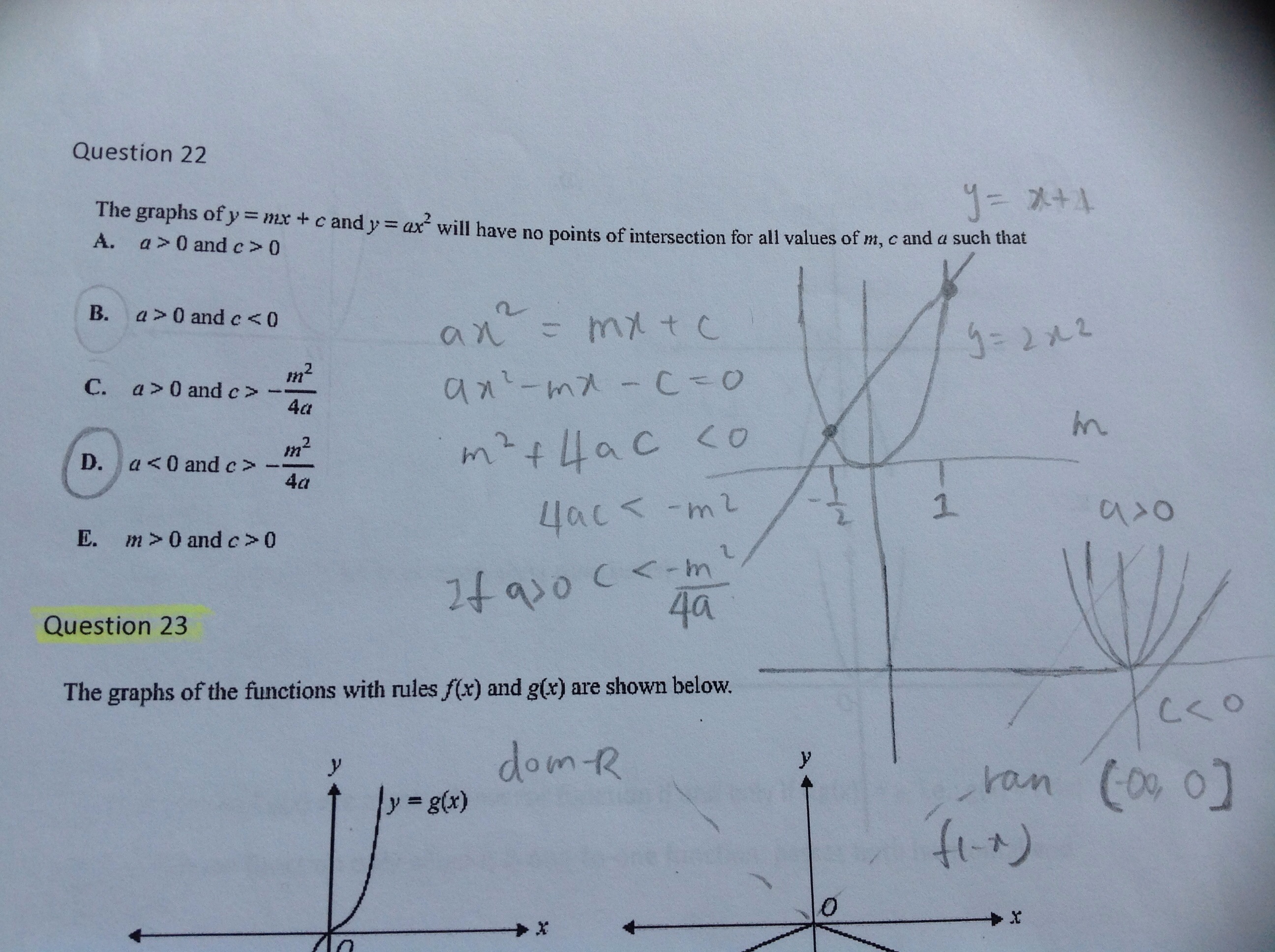
Can someone please explain to me how to do question 22? Thanks!

Answer 1

The answer is (D). Set the two curves equal and solve for `x` to find points of intersection, then deduce the parameter conditions for existence of said points.

Explanation:

To find the points of intersection of the straight line `y=mx+c` and the parabola `y=ax^2`, set their `y` values equal and solve for `x`:

`ax^2=mx+c`
`ax^2-mx-c=0`
`x=(m+-sqrt(m^2+4ac))/(2a)`

We see from this that the curves do not intersect when the discriminant `m^2+4ac<0`. In this case the roots of the quadratic have an imaginary component.

Rearrange this condition:
`m^2+4ac<0`
`4ac<-m^2`

If `a>0`, then
`c<-m^2/(4a)`
If `a<0`, then
`c> -m^2/(4a)`

So the answer is (D). Your written working on the photo shows that you're very nearly there already; you just need to note that when `a` is negative, dividing the inequality through by it changes the inequality direction.
NB There are two parameter regions that work, but only one is listed as an option in the question - they aren't looking for the complete solution of all possible regions, rather for you to say which of their options is part of the complete solution.