Pleas, how solve: Integrade 1/[x^2 Root(9+4x^2)] dx?

2 Answers
Use the substitution
Explanation:
Let
#I=int1/(x^2sqrt(9+4x^2))dx#
Apply the substitution
#I=int1/((9/4tan^2theta)(3sectheta))(3/2sec^2thetad theta)#
Simplify:
#I=2/9intcscthetacotthetad theta#
Integrate directly:
#I=-2/9csctheta+C#
Rewrite in terms of
#I=-2/9 (3sectheta)/(3tantheta)+C#
Reverse the substitution:
#I=-2/9sqrt(9+4x^2)/(2x)+C#
Simplify:
#I=-sqrt(9+4x^2)/(9x)+C#
Explanation:
.
We need to use trigonometric substitution to solve this integral. Let's first set up our right triangle and write the three basic trigonometric functions for our angle
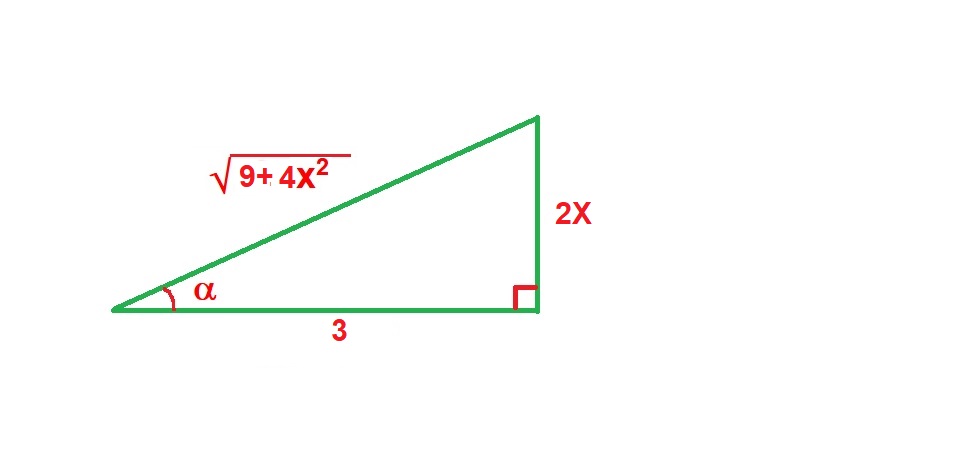
Assigning measurements of
We need to find each of the three pieces in the integral argument in terms of trigonometric functions in order to substitute them in.
From the tangent equation:
From the cosine function:
Taking the derivative of the tangent function, we get:
Now, let's substitute:
Now, we can substitute back for
From the sine function above:

