A triangle has vertices A, B, and C. Vertex A has an angle of #pi/6 #, vertex B has an angle of #(pi)/12 #, and the triangle's area is #12 #. What is the area of the triangle's incircle?

Question

1474 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-20T06:05:54

#color(indigo)("Area of incircle " = A_i = pi * (12/15.5)^2 = 1.88 " sq units"#

#hat A = pi/6, hat B = pi/12, hat C = (3pi) / 4, A_t = 12#

#A_t = (1/2) a b sin C = (1/2) bc sin A = (1/2) ca sin B#

#ab = (2 A_t) / sin C = 24 / sin ((3pi)/4) = 33.94#

#bc = 24 / sin A = 24/ sin (pi/6) = 48#

#ca = 24 / sin C = 24 / sin(pi/12) = 92.73#

#a = (abc) / (bc) = sqrt(33.94 * 48 * 92.73) / 48 = 8.1#

#b = (abc) / (ac) = sqrt(33.94 * 48 * 92.73) / 92.73 = 4.19#

#c = (abc) / (ab) = sqrt(33.94 * 48 * 92.73) / 33.94 = 11.45#

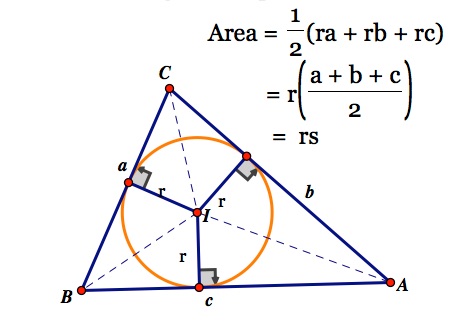
#"Semiperimeter " = s = (a + b + c) / 2 = (8.1 + 4.19 + 11.45) / 2 = 15.5#

#"Incircle radius " = r = A_t / s = 12 / 15.5#

#color(indigo)("Area of incircle " = A_i = pi * (12/15.5)^2 = 1.88 " sq units"#