A triangle has vertices A, B, and C. Vertex A has an angle of #pi/12 #, vertex B has an angle of #pi/8 #, and the triangle's area is #8 #. What is the area of the triangle's incircle?

Question

1821 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-20T06:16:15

#color(purple)("Area of incircle " = A_i = pi * r^2 = 2.44 " sq units"#

#hat A = pi/12, hat B = pi/8, hat C = (19pi) / 24, A_t = 8#

#A_t = (1/2) a b sin C = (1/2) bc sin A = (1/2) ca sin B#

#ab = (2 A_t) / sin C = 16 / sin ((19pi)/24) = 26.28#

#bc = A_t / sin A = 16/ sin (pi/12) = 61.82#

#ca = A_t / sin C = 16 / sin(pi/8) = 41.81#

#a = (abc) / (bc) = sqrt(26.28 * 61.82 * 41.81) / 61.82 = 4.22#

260.63
#b = (abc) / (ac) = sqrt(26.28 * 61.82 * 41.81) / 41.81 =6.24#

#c = (abc) / (ab) = sqrt(26.28 * 61.82 * 41.81) / 33.94 = 7.68#

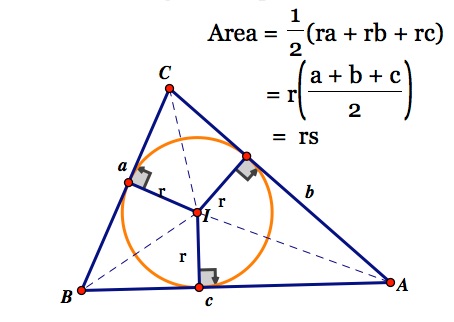
#"Semiperimeter " = s = (a + b + c) / 2 = (4.22 + 6.24 + 7.68) / 2 = 9.07#

#"Incircle radius " = r = A_t / s = 8 / 9.07#

#color(purple)("Area of incircle " = A_i = pi * (8/9.07)^2 = 2.44 " sq units"#