Question

What is the `y`-intercept of `2x - y + 5 = 0`?

Answer 1

The `y`-intercept is at `(0, 5)`.

Explanation:

To find the `y`-intercept, we just plug in `0` for the `x`-value in the equation and find `y`:
`2x - y + 5 = 0`

Plug in `0` for `x`:
`2(0) - y + 5 = 0`

Simplify:
`0 - y + 5 = 0`

`5 - y = 0`

Subtract `color(blue)5` from both sides:
`5 - y quadcolor(blue)(-quad5) = 0 quadcolor(blue)(-quad5)`

`-y = -5`

Divide both sides by `color(blue)(-1)`:
`(-y)/color(blue)(-1) = (-5)/color(blue)(-1)`

Therefore,
`y = 5`

So the `y`-intercept is at `(0, 5)` .

To show that this point is indeed the `y`-intercept, here's a graph of this equation (desmos.com):

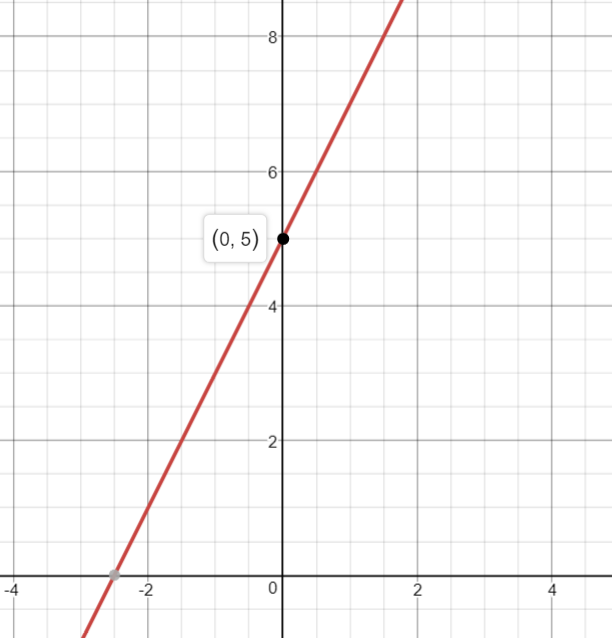
For more information on finding intercepts, feel free to watch this Khan Academy video:

Or visit the Socratic page on intercepts [here].(https://socratic.org/algebra/graphs-of-linear-equations-and-functions/intercepts-by-substitution)

Hope this helps!