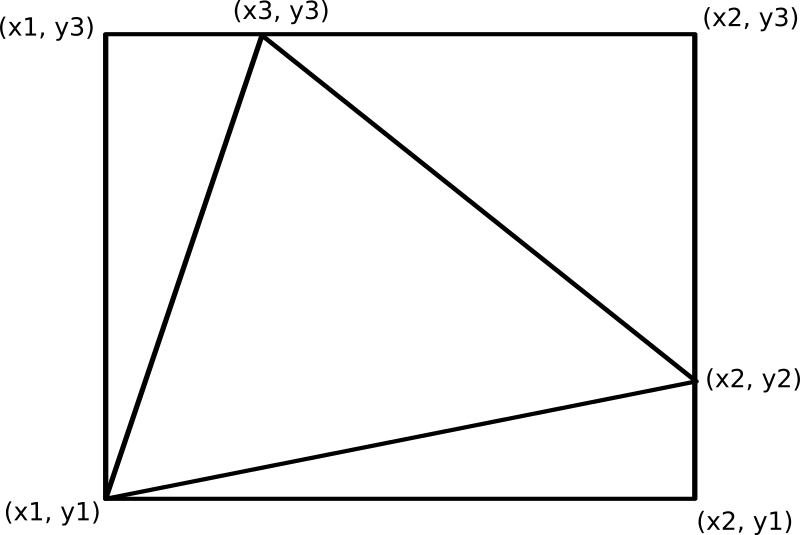
What is the area of a triangle with vertices #(x_1, y_1)#, #(x_2, y_2)#, #(x_3, y_3)# ?

2 Answers
George C.
Oct 18, 2017

#1/2 abs(x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2)#

Explanation:

Given three vertices: #(x_1, y_1)#, #(x_2, y_2)#, #(x_3, y_3)#

Start by assuming:

#x_1 < x_3 < x_2#

#y_1 < y_2 < y_3#

The triangle can be drawn in a rectangle with vertices:

#(x_1, y_1)#, #(x_2, y_1)#, #(x_2, y_3)#, #(x_1, y_3)#

dividing it into #4# triangles, the other #3# of which are:

  • #(x_1, y_1)#, #(x_2, y_1)#, #(x_2, y_2)# with area: #1/2 (x_2-x_1)(y_2-y_1)#

  • #(x_2, y_2)#, #(x_2, y_3)#, #(x_3, y_3)# with area: #1/2 (x_2-x_3)(y_3-y_2)#

  • #(x_3, y_3)#, #(x_1, y_3)#, #(x_1, y_1)# with area: #1/2 (x_3-x_1)(y_3-y_1)#

enter image source here

So the area of the given triangle is:

#(x_2-x_1)(y_3-y_1) - 1/2 (x_2-x_1)(y_2-y_1) - 1/2 (x_2-x_3)(y_3-y_2) - 1/2 (x_3-x_1)(y_3-y_1)#

#=1/2 (x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2)#

Note the symmetry of the final expression. It is symmetric in #(x_1, y_1)#, #(x_2, y_2)#, #(x_3, y_3)# except for its sign.

If we are only interested in the unsigned area of the triangle then we can ignore our initial assumptions and write the universal formula:

#"Area" = 1/2 abs(x_1y_2+x_2y_3+x_3y_1-x_1y_3-x_2y_1-x_3y_2)#

Martin C.
Jun 20, 2018

Just a small comment to the answer from George C.

Explanation:

The answer from George C. is 100% right, even for triangles with such vertices, that they do not fit on a rectangle. An example would be a triangle with the vertices
#(0,0), (2,3), (4,4)#
GeoGebra

Even if the rectangle does not fit, we can still apply the formular and get the solution.

#A=1/2(|0*3+2*4+4*0-0*4-4*3-2*0|)#
#A=1/2(|8-12|)#
#A=1/2(|-4|)#
#A=4/2=2" units"# (confirmed by GeoGebra)

Related questions
Impact of this question
2863 views around the world
You can reuse this answer
Creative Commons License