A triangle has corners at #(3 ,7 )#, #(2 ,5 )#, and #(5 ,4 )#. What is the area of the triangle's circumscribed circle?

Question

3651 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-21T03:41:47

#color(maroon)("Area of circumcircle " = A_c = pi * R^2 = 10.52#

#A(3,7), B(2,5), C(5,4)#

#a = sqrt ((x_b-x_c)^2 + (y_b - y_c)^2)#

#a = sqrt((2-5)^2 + (5-4)^2) = sqrt10#

Similarly, #b = sqrt((5-3)^2 + (4-7)^2) = sqrt13#

#c = sqrt((3-2)^2 + (7-5)^2) = sqrt5#

#"Semiperimeter " = (a + b + c) / 2 = (sqrt10 + sqrt13 + sqrt5) /2 = 4.5#

#A_t = sqrt(s (s-a) (s - b) (s - c))#

#A_t = sqrt(4.5 (4.5 - sqrt10) (4.5 - sqrt13 ) (4.5 - sqrt5)) = 3,49#

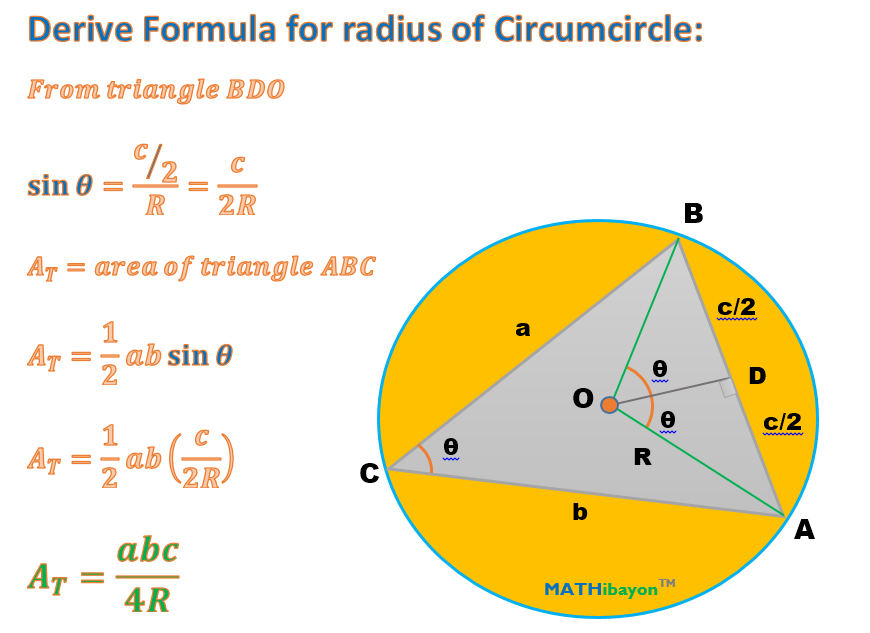
#"circum-radius " = R = (abc) / (4 A_t)#

#R = (sqrt10 * sqrt13 * sqrt5) / (4 * 3.49) = 1.83#

#"Area of circumcircle " = A_c = pi * R^2 = pi * 1.83^2 = 10.52#