A triangle has vertices A, B, and C. Vertex A has an angle of $pi/12$ , vertex B has an angle of $pi/12$ , and the triangle's area is $12$ . What is the area of the triangle's incircle?

Question

1706 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-21T04:46:27

$color(purple)("Area of incircle " = A_i = pi * (12/13.12)^2 = 2.628 " sq units"$

http://jwilson.coe.uga.edu/NCTM%20Boston%20Project/Heron/Introduction.html

$hat A = pi/12, hat B = pi/12, hat C = (5pi) / 6, A_t = 12$

$A_t = (1/2) a b sin C = (1/2) bc sin A = (1/2) ca sin B$

$ab = (2 A_t) / sin C = 24 / sin ((5pi)/6) = 48$

$bc = A_t / sin A = 24/ sin (pi/12) = 92.73$

$ca = A_t / sin C = 26 / sin(pi/12) = 92.73$

$a = (abc) / (bc) = sqrt(48 * 92.73 * 92.73) / 92.73 = 6.93$

$b = (abc) / (ac) = sqrt(48 * 92.73 * 92.73) / 92.73 =6.93$

$c = (abc) / (ab) = sqrt(48 * 92.73 * 92.73) / 48 = 13.38$

$"Semiperimeter " = s = (a + b + c) / 2 = (6.93 + 6.93 + 13.38) / 2 = 13.12$

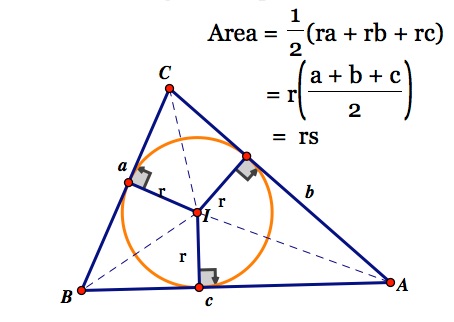
$"Incircle radius " = r = A_t / s = 12 / 13.12$

$color(purple)("Area of incircle " = A_i = pi * (12/13.12)^2 = 2.628 " sq units"$

A triangle has vertices A, B, and C. Vertex A has an angle of pi/12 pi/12 , vertex B has an angle of pi/12 pi/12 , and the triangle's area is 12 12 . What is the area of the triangle's incircle?