Question

`sin^2 63^@ +sin^2 27^@` eqas to why ?

Answer 1

`sin^2 63^@ + sin^2 27^@ = 1`

Explanation:

Note that:

`cos theta = sin (90^@ - theta)`

`cos^2 theta + sin^2 theta = 1`

So we find:

`sin^2 63^@ + sin^2 27^@ = sin^2 (90^@-27^@) + sin^2 27^@`

`color(white)(sin^2 63^@ + sin^2 27^@) = cos^2 27^@ + sin^2 27^@ = 1`

As to why, consider a right-angled triangle with other angles `A` and `B`...

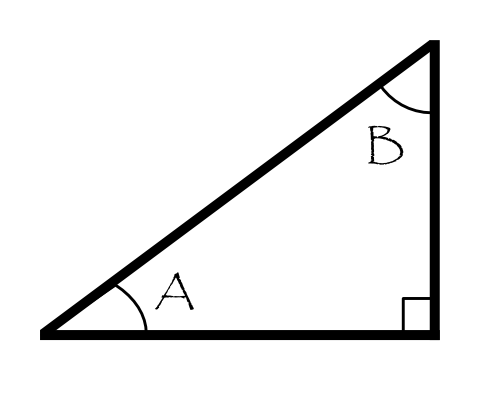
Note that:

• `A+B = 90^@`

• The leg which is `"opposite"` for `A` is `"adjacent"` for `B` and vice versa.

So:

`sin A = "opposite"_A/"hyptotenuse" = "adjacent"_B/"hypotenuse" = cos B = cos (90^@ - A)`