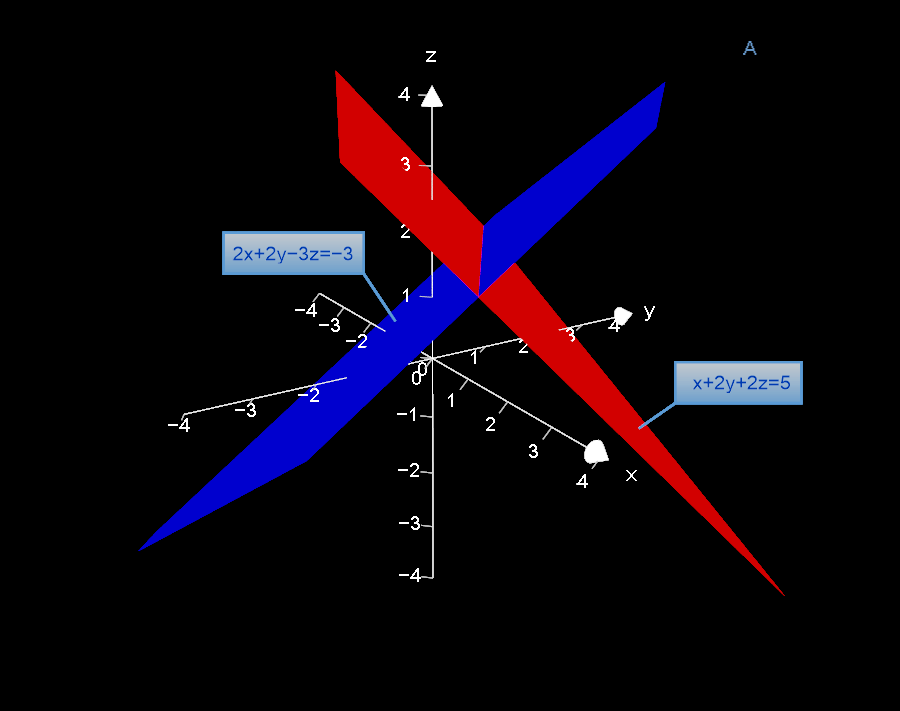
Find the equation of the plane passing through the points (-1,1,1) and (1,-1,1) and perpendicular to the plane x+2y+2z=5 ?

1 Answer
Somebody N.
Jun 23, 2018

#color(blue)(2x+2y-3z=-3)#

Explanation:

We can find the Cartesian equation of a plane by the following:

If we have 3 points in a plane: A, B, C. Then for some point P in the plane with co-ordinates #((x),(y),(z))#:

#vec(AP)=mvec(AB)+nvec(AC)#

Where

#mvec(AB)+nvec(AC)# are vectors in the plane.

If we find a vector normal to the given plane, and this vector be in the plane we seek, then we have a vector in the plane and the 2 given points that lie in the plane.

This normal vector can be found easily from the given equation of the plane.

#x+2y+2z=5#

The normal vector is:

#hat(n)=((1),(2),(2))#

The proof of this can be found here:

https://socratic.org/questions/5a7899f37c01495f160bbd53#547058

Let the given points be:

#A=(-1,1,1), B=(1,-1,1)#

and the normal vector:

#hat(n)=vec(AC)#

Another vector in the plane could be:

#vec(AB)=((2),(-2),(0))#

and we have:

#vec(AP)=((x+1),(y-1),(z-1))#

So:

#vec(AP)=mvec(AB)+nvec(AC)#

#((x+1),(y-1),(z-1))=m((2),(-2),(0))+n((1),(2),(2))#

Form the following equations:

#(x+1)=2m+n \ \ \ \[1]#

#y-1=-2m+2n \ \ \ \[2]#

#z-1=2n \ \ \ \[3]#

We need to eliminate #bbm# and #bbn#.

Add #[1]# and #[2]#:

#x+y=3n \ \ \ [4]#

From #[3]#:

#n=1/2z-1/2#

Substitute in #[4]#

#x+y=3/2z-3/2#

#color(blue)(2x+2y-3z=-3)#

This is the equation of the plane perpendicular to:

#x+2y+2z=5# and containing the points #(-1,1,1)# and #(1,-1,1)#

PLOT:

enter image source here

Related questions
Impact of this question
5779 views around the world
You can reuse this answer
Creative Commons License