I'm pretty sure I already answered this question already, but I'll do it again.
A function #f# is inversible if and only if it is injective. Basically, it is a "one-to-one" function, meaning there exists no two elements in the domain of #f# that are mapped to the same element in the codomain of #f#.
Let #f:X->Y#. Below is an example of an injective function.
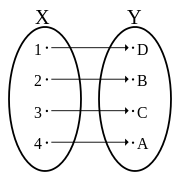
A function is inversible only if it is injective due to the definition of a function.
A function exists if there is no element #a# in its domain such that #f(a)# is multivalued. As such, if #f# is a non-injective function then there must exist #a# and #b# so that #f(a)=f(b)=alpha#. The inverse of #f#, #f^-1#, will map #alpha# to both #a# and #b#, thus making it not a function.
In our particular case, #f(x) = x^2sin(1/x)#.
Let #delta=1/pi# then #epsilon=-1/pi#:
#f(delta) = (color(red)(1/pi))^2sin(1/color(red)(1/pi))=(1/pi)^2sinpi=0#
#f(epsilon) = (color(red)(-1/pi))^2sin(1/color(red)(-1/pi)) = (1/pi)^2sin(-pi)=0#
As such, #f# is not injective and thus doesn't have an inverse.


