Explanation about domain of the function?
#f(x)=(3x-6)/(x^2-4)#
I dont understand why the numbers 2 and -2 are domain of the function
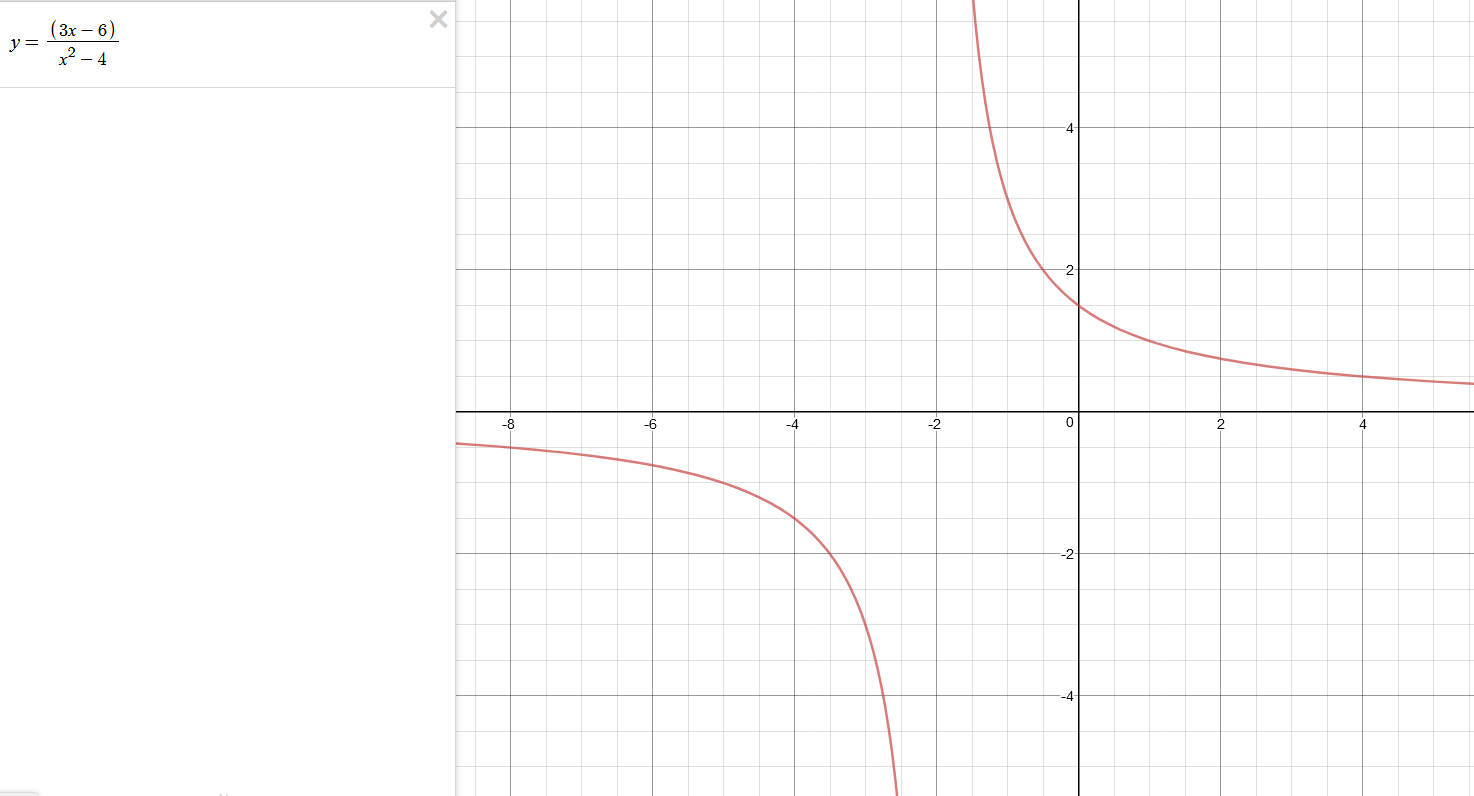
I dont understand why the numbers 2 and -2 are domain of the function

1 Answer
Domain: Every real number except
Explanation:
The domain of a function is the set of all inputs for which the function is defined.
What makes a rational expression, like the one we have, undefined, is when the denominator is equal to zero.
Let's set the denominator of
Since we're dealing with a difference of squares, we can factor this as
Setting both factors equal to zero, we get
These are not in the domain of
The domain of
All this is saying is that the domain of our function includes every real number except for
Hope this helps!

