A triangle has vertices A, B, and C. Vertex A has an angle of #pi/8 #, vertex B has an angle of #(7pi)/12 #, and the triangle's area is #28 #. What is the area of the triangle's incircle?

Question

1434 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-06-30T11:21:17

#color(orange)("Area of inscribed circle " = A_i = pi r^2 = 11.2446#

#"Area of "Delta = A_t = (1/2) a b sin C = (1/2) b c sin A = (1/2) c a sin B#

#"Given " hat A = pi/8, hat B = (7pi)/12, hat C = (7pi)/24, A_t = 28#

#a b = (2 A_t) / sin C = 56 / sin ((7pi)/24) = 70.59#

#b c = (2 A_t) / sin A = 56 / sin (pi/8) = 146.34#

#c a = (2 A_t) / sin B = 56 / sin (7pi)/12) = 57.98#

#a = (a b c) / (b c) = sqrt(70.59 * 146.34 * 57.98) / 146.34= 5.29#

#b = (a b c) / (c a) = sqrt(70.59 * 146.34 * 57.98) / 57.98 = 13.35#

#c = (a b c) / (a b) = sqrt(70.59 * 146.34 * 57.98) / 70.59 = 10.96#

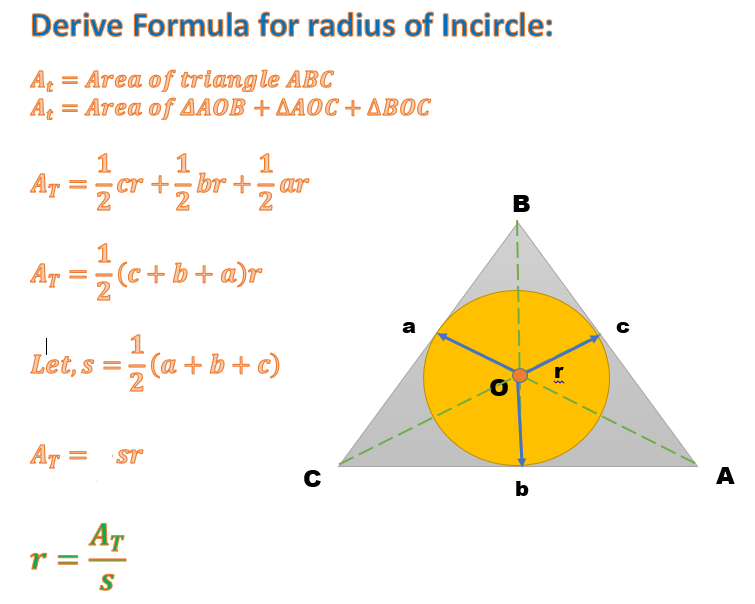
#"Semi-perimeter " = s = (a + b + c) / 2 = 29.6 / 2 = 14.8#

#"Radius of inscribed circle " = r = A_t / s = 28 / 14.8#

#"Area of inscribed circle " = A_i = pi r^2 = pi * (28/14.8)^2 = 11.2446#