Please can you solve the problem on an equation in the real number system given in the image below and also tell the sequence to tackle such problems.?
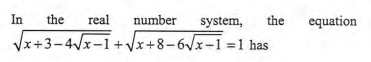 Snapshot from book
Snapshot from book
- No Solution.
- Exactly two distinct solutions
- Exactly 4 distinct solutions.
- Infinitely many solutions
Snapshot from book
- No Solution.
- Exactly two distinct solutions
- Exactly 4 distinct solutions.
- Infinitely many solutions
1 Answer
Explanation:
Since
let try then
so it's not D.
Now try
Now try
We can see that when we will take more
That to say
will give us a solution in
So I think it must be only 1 solution correct.
Alternative way is this:
Given we're "living" in
you need to repeat the idea again and again until the "

