Question

What is the equation in standard form of the parabola with a focus at (14,-19) and a directrix of y= -4?

Answer 1

`(x-14)^2=30(y+11.5)`

Explanation:

Given -

Focus `(14, -19)`
Directrix `y=-4`

Find the equation of the parabola.

Look at the graph.

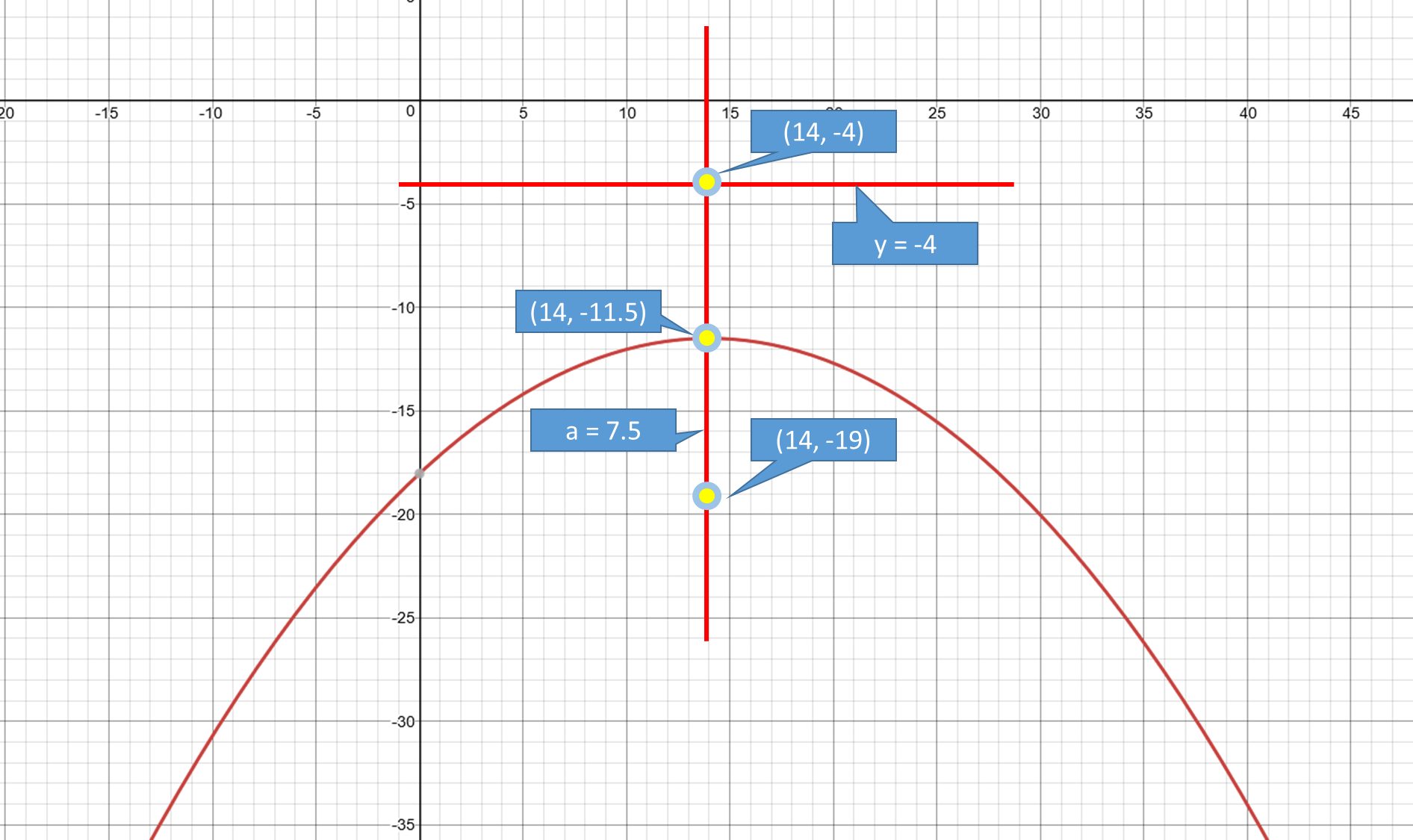
From the given information, we can understand the parabola is facing downward.

The vertex is equidistance from directrix and focus.

Total distance between the two is 15 units.
Half of 15 units is 7.5 units.

This is `a`

By moving down 7.5 units down from `-4`, you can reach point `(14, -11.5)`. This is vertex

Hence vertex is `(14,-11.5`

The vertex is not at the origin. Then, the formula is

`(x-h)^2=4a(y-k)`

Plug in the values.

`(x-14)^2=4(7.5)(y+11.5)`

`(x-14)^2=30(y+11.5)`