Question

A block of mass m=2kg is kept in position on the wall by applying an oblique force 'F' at 60° to the vertical as shown . calculate the minimum value of 'F'(the coafficient of friction between the wall and the block = 0.9) (Take 'g'=10ms^-2)?

Answer 1

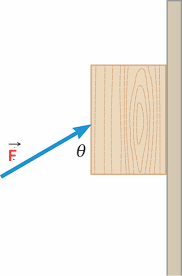
Let the force `vecF` be applied on the block obliquely at an angle of `theta=60^@` with the vertical as shown in the figure above.

The resolved part of the applied force `vecF` perpendicular to the wall will be `vecFsintheta` and the resolved part parallel to the wall in upward direction is `vecFcostheta`

So static fictional force in upward direction is

`F_suarr="coefficient of friction"(mu_s)xxFsintheta`

`=0.9vecFsintheta`

So considering the equilibrium of forces we have

`vecFcostheta+0.9*vecFsintheta=mg`

`=>vecFcos60+0.9*vecFsin60=2*10`

`=>vecF=20/(1/2+(0.9sqrt3)/2)~~15.6N`

If the applied force `vecF` acts obliquely downward making an angle `theta=60^@` with the vertical then the component of `vecF` in vertical direction will be downward and equilibrium of force will give the following relation.

`0.9*vecFsintheta=mg+ vecFcostheta`

`=>-vecFcos60+0.9*vecFsin60=2*10`

`=>vecF=20/(-1/2+(0.9sqrt3)/2)~~71.6N`