A triangle has corners at #(2 ,5 )#, #(3 ,1 )#, and #(4 ,2 )#. What is the area of the triangle's circumscribed circle?

Question

3346 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-07-10T15:51:58

#color(orange)("Area of Circum circle " A_R = pi R^2 = pi * 2.1024^2 = 13.8861 " sq units"#

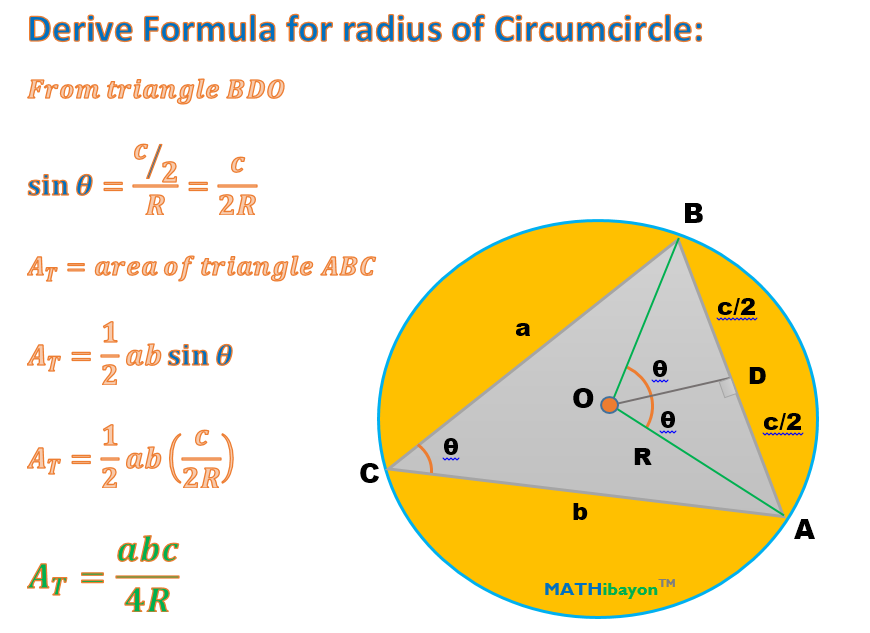
#"Area of Triangle " = A_T = (a b c) / (4 R)#

#A (2,5), B (3,1), C(4,2)#

#a = sqrt((2-3)^2 + (5-1)^2) = sqrt 17 = 4.1231#

#b = sqrt((3-4)^2 + (1-2)^2) = sqrt 2 = 1.4142#

#c = sqrt((4-2)^2 + (2-5)^2) = sqrt 13 = 3.6056#

#"Semi perimeter of the triangle " s = (a + b + c ) / 2 = 4.5715#

#A_T = sqrt (s (s-a) (s-b) (s - c))#

#A_T = sqrt(4.5715 (4.5715 - 4.1231) (4.5715 - 1.4142) (4.5715 - 3.6056)) = 2.5#

#R = (a b c ) / (4 * A_T) = (sqrt 17 * sqrt 2* sqrt 13) / (4 * 2.5) = 2.1024#

#color(orange)("Area of Circum circle " A_R = pi R^2 = pi * 2.1024^2 = 13.8861 " sq units"#