Question

A triangle has corners at `(4 ,6 )`, `(2 ,9 )`, and `(7 ,5 )`. What is the area of the triangle's circumscribed circle?

Answer 1

The area of the triangle's circumscribed circle`=Delta=85.4329` sq. units.

Explanation:

Let `triangleABC " be the triangle with corners at"`

`A(4,6) ,B(2,9) and C(7,5)`

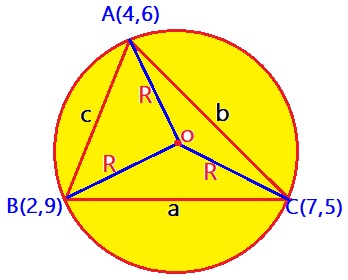
Using Distance formula ,we get

`a=BC=sqrt((2-7)^2+(9-5)^2)=sqrt(25+16)=sqrt41`

`b=CA=sqrt((4-7)^2+(6-5)^2)=sqrt(9+1)=sqrt10`

`c=AB=sqrt((4-2)^2+(6-9)^2)=sqrt(4+9)=sqrt13`

Using cosine Formula ,we get

`cosB=(c^2+a^2-b^2)/(2ca)=(13+41-10)/(2sqrt13sqrt41)=22/(sqrt533`

We know that,

`sin^2B=1-cos^2B`

`=>sin^2B=1-484/533=49/533`

`=>sinB=7/sqrt533to[because Bin(0 ^circ,180^circ)]`

Using sine formula:we get

`b/sinB=2R=>R=b/(2sinB)`

`=>R=sqrt10/(2 (7/sqrt533))=(sqrt10xxsqrt533)/(2*7)~~5.2148`

So , the area of the triangle's circumscribed circle is:

`Delta=piR^2=pi*(5.2148)^2~~85.4329 ,sq.units`