The graph y=(x^2+5x+7)/(x+2) is shown below. Find the value of the product abcd?
The dashed vertical line through D (d,0) is a vertical asymptote. The dashed line BC is a slant asymptote. The coordinates of B and C are B(0,b) and C(c,0). The curve crosses the y-axis at A(0,a).
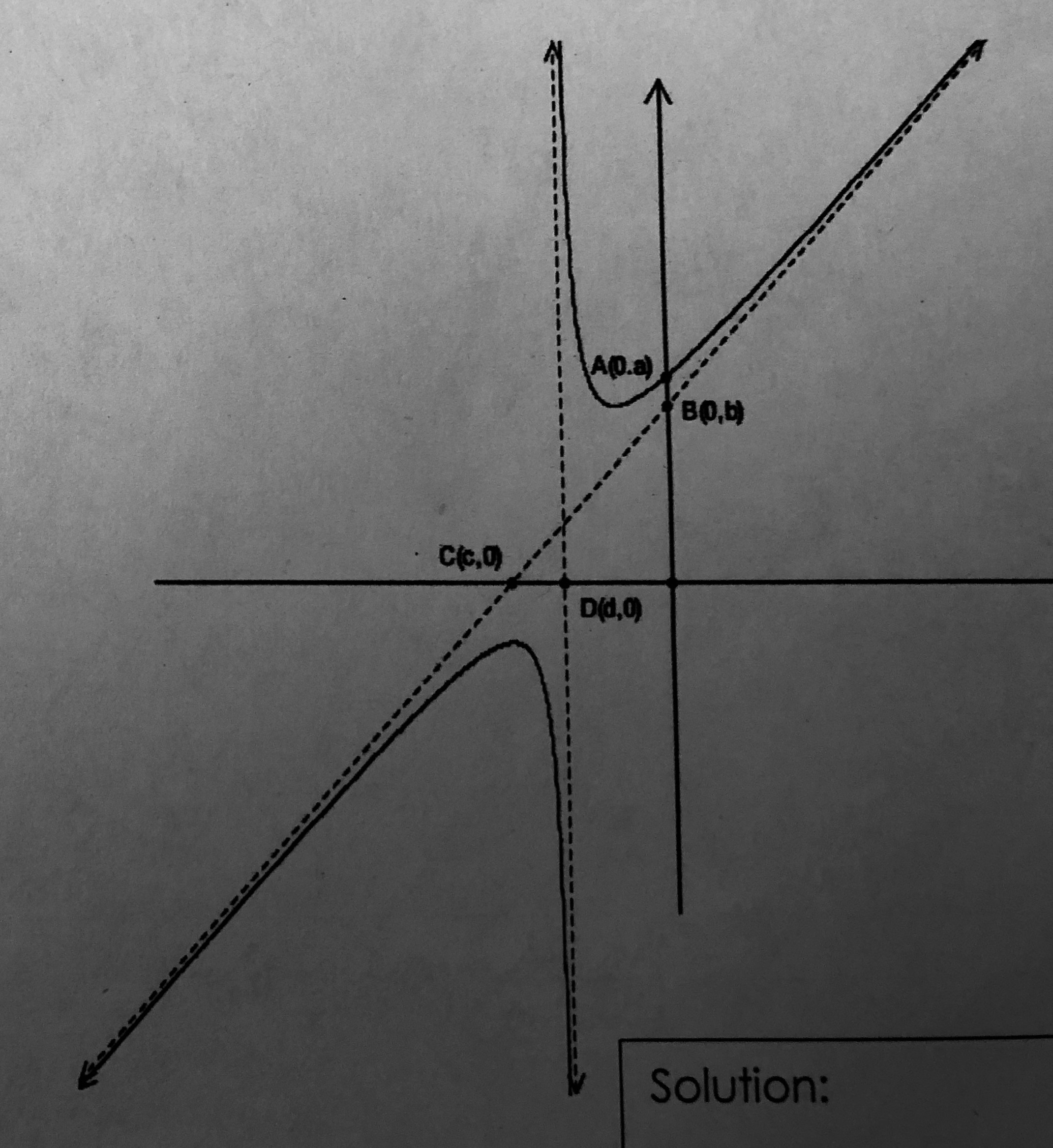
The dashed vertical line through D (d,0) is a vertical asymptote. The dashed line BC is a slant asymptote. The coordinates of B and C are B(0,b) and C(c,0). The curve crosses the y-axis at A(0,a).

1 Answer
Explanation:
The question asks us to find various properties of the curve and combine them.
1) Vertical asymptote,
Find the vertical asymptote by setting the denominator to 0:
Check that the numerator is not also 0 at the same point:
So this point is not a function hole.
2) Curve y-intercept,
We seek the function value
3) Slant intercept
Use polynomial long division to express
Divide leading terms:
Repeat:
So
We know from this that the slant asymptote line is
4) Slant intercept
For the
For the
5) Combine results
From above,
So
