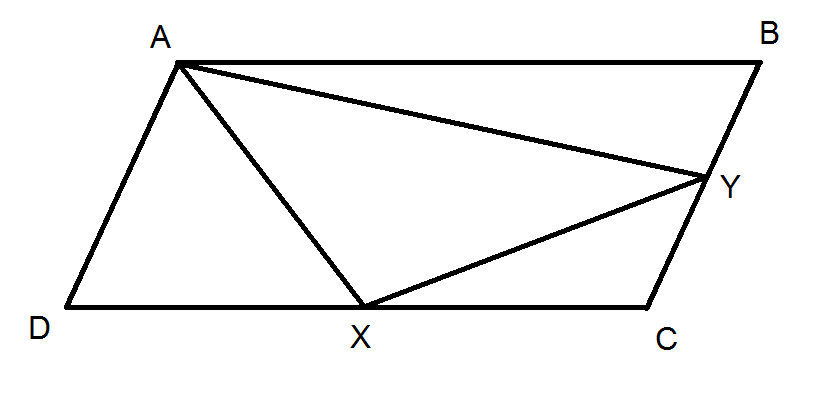
Here is our situation, visualised:
To solve this, we'll need to use two formulas:
- For the area of a triangle: #A_Delta=1/2 ab sinC#
*For the area of a parallelogram: #A_square=ab sinC#
The area of #AXY# can be written as the difference of more areas:
#"Area"(AXY) = "Area"(ABCD) - "Area"(ADX) - "Area"(XCY) - "Area"(YBA)#
Instead of #"Area"(...)#, I'm going to use #A_(...)#:
#A_(AXY) = A_(ABCD) - A_(ADX) - A_(XCY) - A_(YBA)#
Let #a=AB=CD# and #b=BC=DA#, as well as #alpha# to be the angle of vertex #A#. Note that:
#sinA=sinalpha=sinC#
#sinB=sin(180^@-alpha) = sinalpha=sinD#
#:. sinA=sinB=sinC=sinD=sinalpha#
We have to use our established formulae:
#A_(ABCD) = ab sinalpha#
#A_(ADX)= 1/2(a/2)b sinalpha=1/4ab sinalpha=1/4 A_(ABCD)#
#A_(XCY)=1/2(a/2)(b/2) sinalpha = 1/8 ab sinalpha=1/8 A_(ABCD)#
#A_(YBA) = 1/2a(b/2) sinalpha = 1/4 ab sinalpha = 1/4 A_(ABCD)#
#=> A_(AXY) = A_(ABCD) - 1/4 A_(ABCD) - 1/8 A_(ABCD) - 1/4 A_(ABCD) = 3/8 A_(ABCD)#
#color(red)("Area"(AXY) = 3/8 "Area"(ABCD))#

