Let S be a square of unit area. Consider any quadrilateral which has one vertex on each side of S. If a,b,c and d denote the lengths of sides of the quadrilateral, prove that 2<=a^2+b^2+c^2+d^2<=4?
1 Answer
Jul 15, 2018
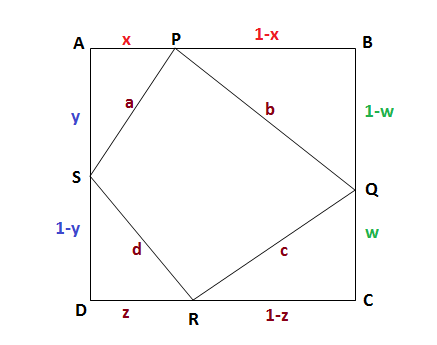 drawn
drawn
Let
So
Let
Applying Pythagoras thorem we can write
Now by the problem we have
Hence

