Points A and B are at #(2 ,2 )# and #(3 ,7 )#, respectively. Point A is rotated counterclockwise about the origin by #pi/2 # and dilated about point C by a factor of #3 #. If point A is now at point B, what are the coordinates of point C?
2 Answers
Explanation:
New coordinates of A after
Explanation:
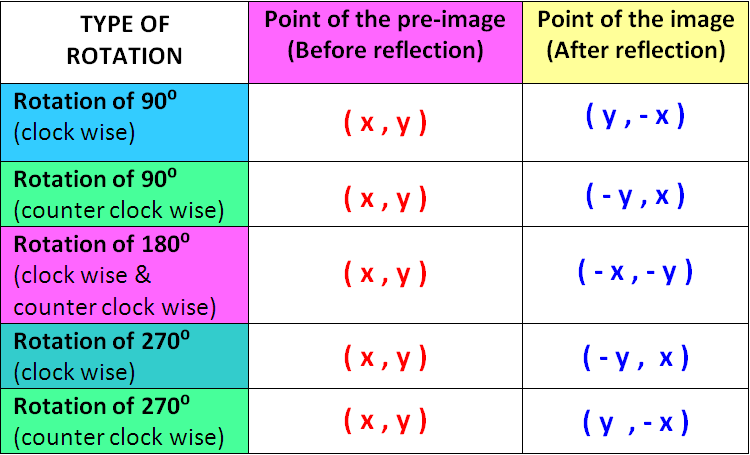
#"under a counterclockwise rotation about the origin of "pi/2#
#• " a point "(x,y)to(-y,x)#
#A(2,2)toA'(-2,2)" where A' is the image of A "#
#vec(CB)=color(red)(3)vec(CA')#
#ulb-ulc=3(ula'-ulc)#
#ulb-ulc=3ula'-3ulc#
#2ulc=3ula'-ulb#
#color(white)(2ulc)=3((-2),(2))-((3),(7))#
#color(white)(2ulc)=((-6),(6))-((3),(7))=((-9),(-1))#
#ulc=1/2((-9),(-1))=((-9/2),(-1/2))#
#rArrC=(-9/2,-1/2)#
