Question

Three candidates are selected from a certain number of interviewees.If the order is not taken into account, then number of ways the candidates can be chosen is 35.How many ways are there if the order is taken into account?

Answer 1

`210` ways

Explanation:

We know that if the order is not taken into account, we have `nC_3=35` as we don't know the set size

To go from Combinations to permutations for a specific problem:

`nP_r= nC_r*r!`

So if the order did matter:

`nP_3= 35*3! = 210` ways

Answer 2

An alternate approach

Explanation:

Since combinations results can be read straight off of Pascal's Triangle, we can look at the triangle to find where choosing 3 from a population gives 35:

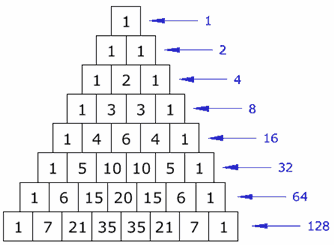
On the bottom line we can see that choosing 3 from a population of 7 gives 35. So we have in our question:

`35=(7!)/(3!4!)=C_(7,3)`

To put order into the calculation, we can find the permutation of 7 and 3:

`P_(7,3)=(7!)/(4!)=7xx6xx5=210`