Question

Prove that if lengths of 2 medians of a triangle are equal then the triangle is isosceles ?

Answer 1

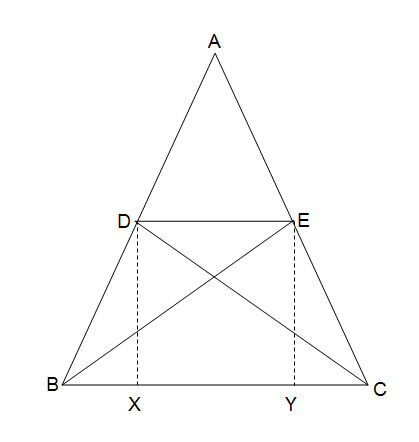
Given

In `Delta ABC`, D and E are mid points of AB and AC.

Two medians `BE=CD`.

RTP: `Delta ABC` is isosceles.

Construction

`D,E` are joined. `DX and EY` are two perpendiculars drawn on BC.

Proof

`D and E` being mid points of `AB and AC` , the line `DE` must be parallel to `BC`. Hence perpendiculars `DX=EY`

Now in `DeltaCDXand Delta BEY`

`angle BYE=angleCXD=90^@`

`BE=CD`. given

and

`DX=EY` proved

`DeltaCDX~=Delta BEY` following `RHS` rule.

So
`angle EBY=angleDCXor angle EBC=angleDCB`

Now in `DeltaDCBand DeltaEBC` we have

`BE=CD`.given

`BC` common

and

`angle EBC=angleDCB`

So `DeltaDCB~= DeltaEBC` by SAS rule

So `angleDBC= angleECB`

`=>angleABC= angleACB`

This means `Delta ABC` is isosceles.