A triangle has corners at #(2 ,8 )#, #(3 ,6 )#, and #(4 ,7 )#. What is the area of the triangle's circumscribed circle?

Question

1347 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-07-26T06:45:48

#"The area of the triangle's circumscribed circle is :"#
#Delta=piR^2=pi*(sqrt50/6)^2=pi(50/36)~~4.3633 ,sq.units#

Let #triangle ABC # be the triangle with corners at

#A(2,8)B(3,6) and C(4,7)#

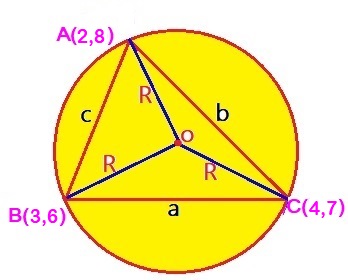
enter image source here

#a=BC=sqrt((7-6)^2+(4-3)^2)=sqrt(1+1)=sqrt2#

#b=CA=sqrt((8-7)^2+(2-4)^2)=sqrt(1+4)=sqrt5#

#c=AB=sqrt((8-6)^2+(2-3)^2)=sqrt(4+1)=sqrt5#

#cosB=(c^2+a^2-b^2)/(2ca)=(5+2-5)/(2sqrt5sqrt2)=2/(2sqrt10)=1/sqrt10#

We know that,

#sin^2B=1-cos^2B#

#=>sin^2B=1-1/10=9/10#

#=>sinB=3/(sqrt10)to[because Bin(0 ^circ,180^circ)]#

Using sine formula:we get

#b/sinB=2R=>R=b/(2sinB)#

#=>R=sqrt5/(2(3/sqrt10))=(sqrt50)/(6)~~1.1785#

So , the area of the triangle's circumscribed circle is:

#Delta=piR^2=pi*(sqrt50/6)^2=pi(50/36)~~4.3633 ,sq.units#