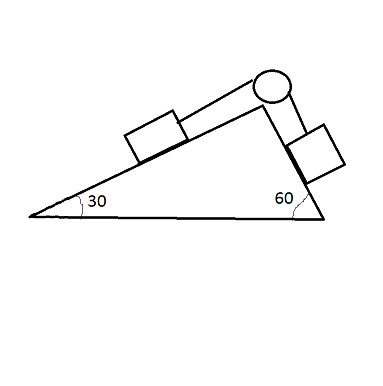
Two blocks A and B of equal masses are attached to a string passes over a smooth pulley fixed to a wedge as shown find the magnitude of acceleration of the center of mass of the two blocks when they are released from rest . neglect friction ?
1 Answer
Explanation:
I am going to add 3 words to the question:
"magnitude of the acceleration of the center of mass".
Assume that mass A is on the left and mass B is on the right. Define right to be positive direction (for force, and acceleration).
The component of each block's weight parallel with the respective incline:
W_A = -m*g*sin30^@
W_B = m*g*sin60^@
The weights are translated to upward pull on the string. Therefore, the net force acting on the each mass along the respective incline:
Mass A
F_"netA" = -W_A + W_B = -m*g*sin30^@ + m*g*sin60^@
F_"netA" = m*g*(-sin30^@ + sin60^@)
F_"netA" = m*g*(-0.5 + 0.866) = 0.366*m*g
Mass B
F_"netB" = -W_A + W_B = -m*g*sin30^@ + m*g*sin60^@
F_"netB" = m*g*(-sin30^@ + sin60^@)
F_"netB" = m*g*(-0.5 + 0.866) = 0.366*m*g
Acceleration of A:
F_"netA" = m*a_A
a_A = F_"netA"/m = (0.366*cancel(m)*g)/cancel(m)
Notice that if you go thru the same calculation for B, you get the same result. Therefore the center of mass will accelerate at
I hope this helps,
Steve

