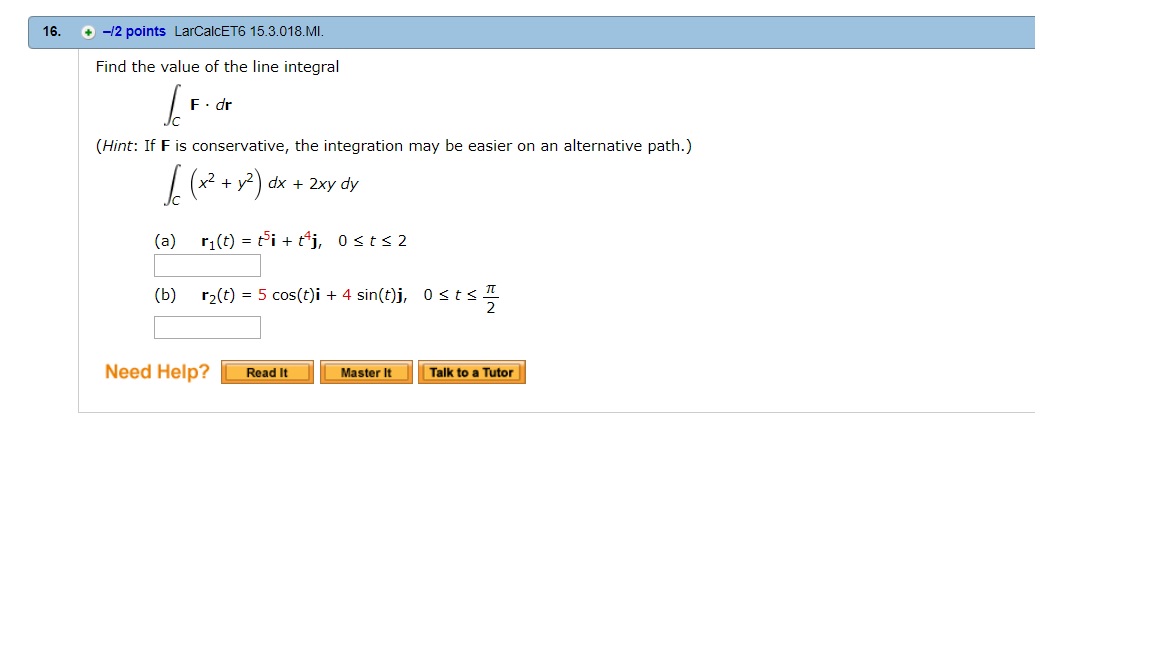
#bbF(bbr) = (:x^2 + y^2,2xy:)#
#"curl " bbF = det[(del_x, del _y),(x^2 + y^2,2xy)] = bb0#
Hence #bbF# is conservative and line integrals are path-independent.
#bbr_1 = t^5 bbi + t^4 bbj qquad qquad 0 le t le 2#
So that path is: #(0,0) to (2^5, 2^4)#
An alternative path is:
#bbr = t bbi + t/2 bbj qquad qquad 0 le t le 2^5 qquad qquad bbr^' = bbi + 1/2bbj#
#int_C bb F(bbr) * d bb r = int_C bbF(bbr (t)) * bbr ^' \ dt#
# = int_(0,2^5) (: t^2 + t^2/4, t^2 :) * (:1 , 1/2 :) \ dt#
#= int_(0,2^5) 7/4t^2 \ dt = 57344/3#
#bbr_2 = 5 cos t bbi + 4 sint bbj qquad 0 le t le pi/2#
Which is: #(5,0) to (0,4)#
As much simpler calculation will follow from this 2 step approach:
- #{(bbbA qquad (5,0) to (0,0), dy = y = 0),(bbbB qquad (0,0) to (0,4) , dx = x = 0 ):}#
#triangle = int_(Delta x) x^2 + y^2 \ dx + int_(Delta y) 2xy \ dy#
#triangle = int_(5,0) (x^2 + cancel(y^2) ) dx + cancel( int 2xy \ dy)#
# = [x^3/3]_(5,0) = - 125/3 #
#triangle = cancel( int (x^2 + y^2 ) dx) + int_(0,4) 2cancel(x)y \ dy = 0#
#C_2 = bbbA + bbbB = - 125/3#