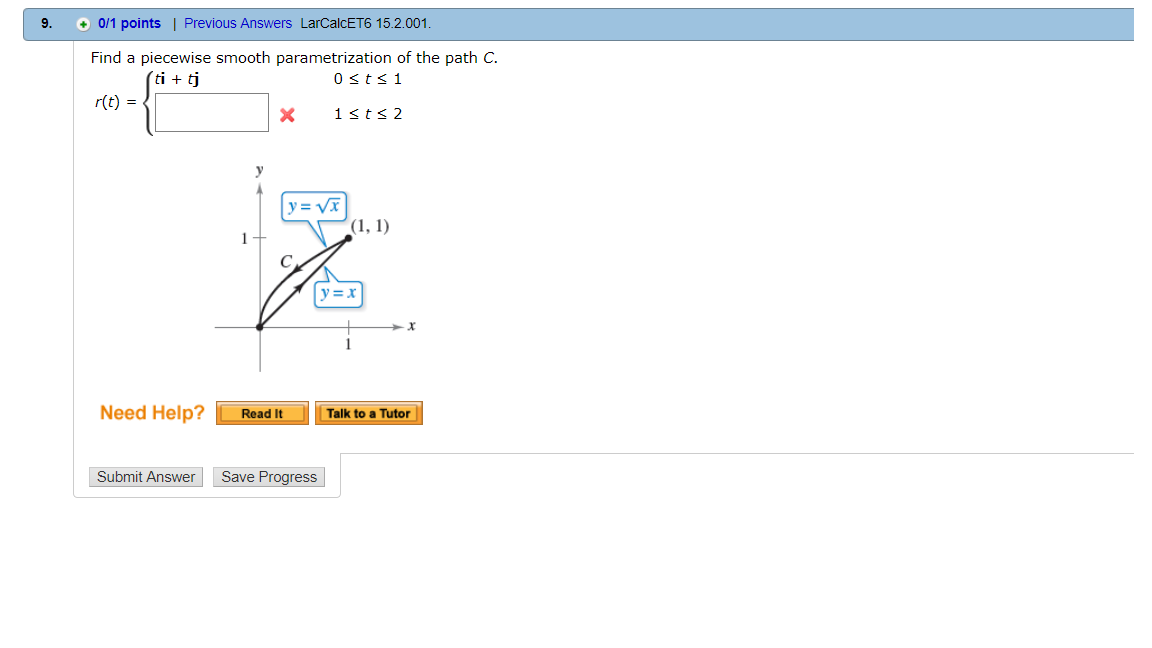
Find a piecewise smooth parametrization of the path C. r(t) = ti + tj 0 ≤ t ≤ 1 _____????______ 1 ≤ t ≤ 2?
1 Answer
Aug 5, 2018
Explanation:
Note that the curved portion of the curve
If it were parameterised from
r(t) = that(i)+t^2hat(j)
As it is, we want to parameterise it in the opposite direction for
Hence we want:
r(t) = (2-t)hat(i)+(2-t)^2hat(j)
So the piecewise parameterisation can be written:
r(t) = { (that(i)+that(j) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ " for " 0 <= t <= 1), ((2-t)hat(i)+(2-t)^2hat(j) " for " 1 <= t <= 2) :}

