Here is my second question on the complex numbers assignment. How do I prove the following below?

If z=cos#theta#+isin#theta#, prove that;
1. 1+#z+z^2#=(1+#cos theta)(cos theta+isin theta)#
2. #z//(1+z)=1+itan(theta//2)#

2 Answers
Hriman
Aug 10, 2018

See below

Explanation:

  1. #z= costheta+isintheta#

#z+1= costheta+isintheta+1#

#(z+1)^2=(costheta+isintheta+1)^2#

#1+2z+z^2= cos^2theta+2costhetaisintheta+2costheta+i^2sin^2theta+2isintheta+1#

#1+2z+z^2= cos^2theta+2costhetaisintheta+2costheta-sin^2theta+2isintheta+sin^2theta+cos^2theta#

#1+2z+z^2= 2cos^2theta+2costhetaisintheta+2costheta+2isintheta#

Factor:
#1+2z+z^2= 2(1+costheta)(costheta+isintheta)#

Ultrilliam
Aug 10, 2018

You asked this:

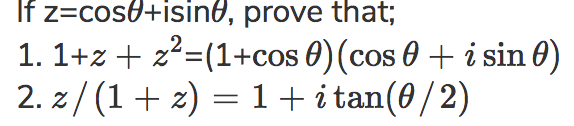
enter image source here

For 1), you are proving that:

  • #1 + z + z^2 = z(1 + cos theta) qquad equiv qquad 1/z + 1 + z = 1 + cos theta#

#z# is the unit circle so I don't see a problem with dividing like that.

Well:

#qquad 1/z = barz/(z bar z) = (cos theta - i sin theta)/(cos^2 theta + sin^2 theta) = cos theta - i sin theta#

So:

#qquad 1/z + 1 + z = cos theta - i sin theta + 1 + cos theta + i sin theta#

#qquad = 2cos theta + 1 #

#implies 1 + z + z^2 = (1 + bb2 cos theta)(cos theta + i sin theta)#

That's not what you're looking for but it is the same as other answer posted here for this question, if you actually finish off the algebra.

For 2) , I think the answer is out by a factor of 2:

#z/(1 + z) = (1 + z - 1)/(1+z)#

#= 1 - 1/(1+z)#

#= 1 - bar(1+z)/((1+z) bar((1+z)))#

#= 1 - (1 + cos theta - i sin theta )/((1 + cos theta)^2 + sin^2 theta)#

#= 1 - (1 + cos theta - i sin theta )/(2 + 2 cos theta )#

#= 1/2 + i( sin theta )/(2 + 2 cos theta )#

Half angle formulae:

#= 1/2 + i( 2 sin (theta/2) cos (theta/2) )/(2 + 2 (2 cos^2 (theta/2) - 1) )#

#= 1/2 + i( 2 sin (theta/2) cos (theta/2) )/( 4 cos^2 (theta/2) )#

#= bb(1/2)(1 + i tan (theta/2) )#

Again not the answer you're looking for but I don't see the mistake in the algebra.

Related questions
Impact of this question
2306 views around the world
You can reuse this answer
Creative Commons License