Marginal product and diminishing returns

Key Questions

  • What is a marginal product return?

    Answer:

    Marginal Product shows the rate of change of Total Product.

    Explanation:

    This concept is used in the 'Law of Variable Proportions' or 'Law of Diminishing Returns to a variable factor'. First Refer the Table.

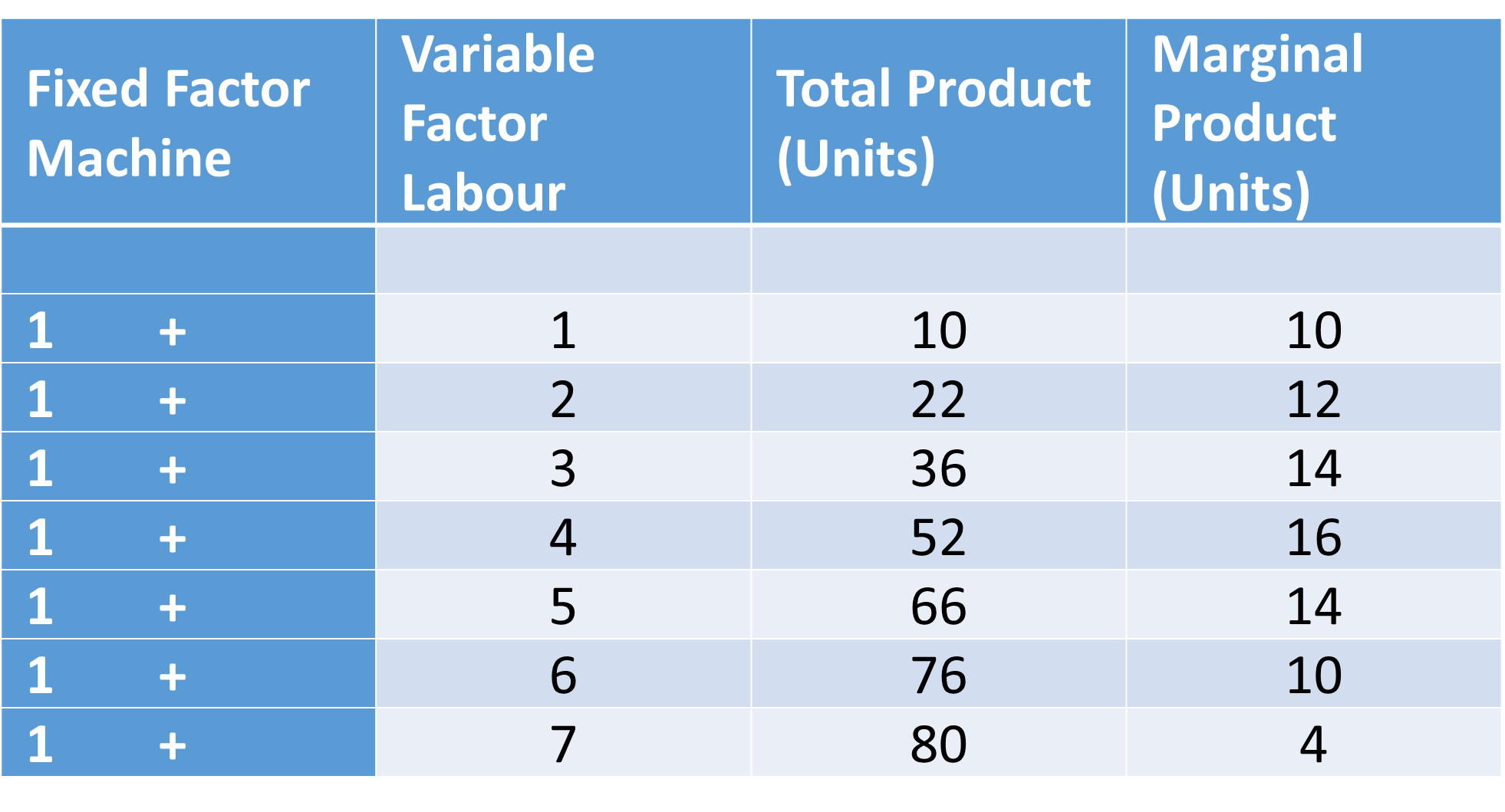
    enter image source here

    In the production both fixed factor [Machine] and variable factor are employed. Fixed factor is kept unchanged at 1 unit. Labour is added one after another and we examine what happens to Total Product.
    When one labourer is employed the Total product is 10 units. This is the present Total Product.
    What is the Total Product when no labourers was employed? It is zero. It is the previous total.
    Marginal Product = Present Total Product - Previous Total Product.
    So, Marginal Product of the 1st labourer is #10-0=10 # units

    We employ one more labourer. After taking the 2nd labourer the Total Product becomes 22. This is the present total, now. The previous total is 10 units. To find the Marginal product of the 2nd labourer, apply the formula -

    Marginal Product = Present Total Product - Previous Total Product.

    Marginal Product is #22-10=12# units. You apply this formula to find the Marginal Product of the 3, 4, 5, 6 and 7 th labourers. You will get 14, 16, 14, 10 and 4.

    Now Let us go the definition. When the producer increases his labourer from 4 to 5 the Total Product increases from 52 to 66. What is the rate of increase of the Total Product? It is = New Total - Old Total, i.e., #66 - 52 = 14# That 14 is the Marginal Product of the 5th labourer.

    Marginal Product can also be defined as the net increase in Total Product due to an addition of one unit of variable factor.

    Marginal product can also be viewed as the change in Total Product due to a unit change in variable factor. In our case
    #MP =( DeltaTP)/(Delta L)#

    You, please, watch the video lesson also -Marginal Product

    Nallasivam V · 1 · Sep 21 2015

Questions

Production and Costs in Product Markets