Planes
Key Questions
-
It can be said that those planes are parallel.
You are here in a typical "sandwich" situation:
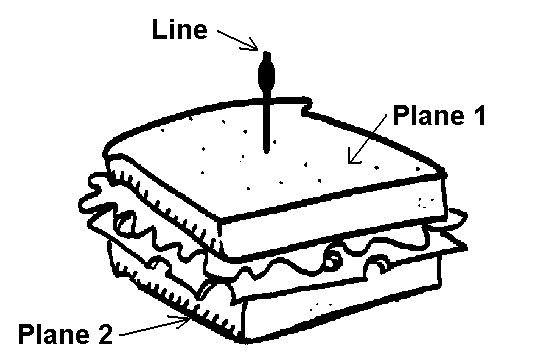
(Picture source: http://school.discoveryeducation.com/clipart/clip/sandwich.html)Your planes are the slices of bread. Both of them are perpendicular to the same line (the toothpick).
As in the sandwich the first slice of bread must form an angle of 90° all around the toothpick; the second slice also must have the same property.
As in the sandwich the two slices of bread will never "bend" to meet each other otherwise you'll have the "tortilla" effect!!!!

(Picture source: http://www.dunbarsystems.com/baked-unbaked-products/tortillas/default.html) -
Answer:
Any three noncollinear points make up a plane.
Explanation:
Two distinct points,
#"A"# and#"B"# , determine a unique line in space.A third point
#"C"# not on this line determines a unique plane that we can denote as#"ABC"# .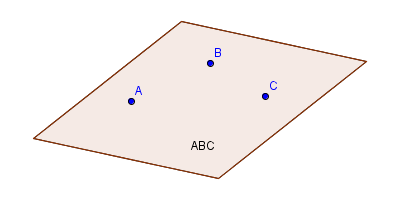
-
Answer:
Given two lines, they define a plane only if they are:
parallels non coincident or non coincident intersecting.Explanation:
Given two lines, they define a plane only if they are:
parallels non coincident or non coincident intersecting. If they are parallels, taking a point in one of them and the support of the other we can define a plane. If they intersect, with the normal to both directions and their intersection point, a plane can also be constructed.#1)# Parallel#r_1->p = p_1 + lambda_1 vec v#
#r_2->p = p_2 + lambda_2 vec v# #p_1^0 = p_1 + lambda_1^0 vec v#
#p_2^0 = p_2 + lambda_2^0 vec v# #vec w = vec v xx (p_1^0-p_2^0) =vec v xx (p_1-p_2)# the plane equation is given by
#Pi_1-><< vec w, (p-p_1)>> = << vec w, (p-p_2)>> = 0# here
#p = {x,y,z}# #2)# IntersectingSolve for the intersection point
#p_0# #p_0 = p_1 + lambda_1 vec v_1 = p_2 + lambda_2 vec v_2# Once obtained
#p_0# the plane is built as follows#vec w = vec v_1 xx vec v_2# #Pi_2 -> << vec w, (p-p_0) >> = 0# -
The Cartesian equation of a plane
#P# is#ax + by + cz + d = 0# , where#a, b, c# are the coordinates of the normal vector#vec n = ( (a), (b), (c) ) # Let
#A, B and C# be three noncolinear points,#A, B, C in P#
Note that#A, B and C# define two vectors#vec (AB)# and#vec (AC)# contained in the plane#P# . We know that the cross product of two vectors contained in a plane defines the normal vector of the plane.Now, we can use an example to illustrate the solution. Assume that the coordinates of the three points are the following:
#A(1,2,3), B(-2,1,0)# and#C(0,3,2)# From the coordinates of the points
#A, B# and#C# we can find the vectors#vec (AB)# and#vec (AC)# :#vec (AB) = (x_b - x_a)*hat i + (y_b - y_a)*hat j + (z_b - z_a)*hat k#
#vec (AC) = (x_c - x_a)*hat i + (y_c - y_a)*hat j + (z_c - z_a)*hat k#
where#hat i, hat j# and#hat k# are the unit vectors on the cartesian axes of coordinates#Ox, Oy# and#Oz# .After plugging in the values of the coordinates, we have:
#vec (AB) = (-2 - 1)*hat i + (1-2)*hat j + (0-3)*hat k#
So,#vec (AB) = -3 hat i - hat j -3 hat k# #vec (AC) = (0-1)*hat i + (3-2)* hat j + (2-3)*hat k# .
So,#vec (AC) = -hat i + hat j - hat k# Next, we'll find the normal vector from the cross product of
#vec (AB)# and#vec (AC)# #vec n = vec (AB)# x#vec (AC) = | (hat i,hat j,hat k),(-3,-1,-3),( -1,1,-1)|# #=# # 4 hat i - 4 hat k# Therefore, the equation of the plane is
#4x-4z+d=0# . In order to find#d# , we can plug in the coordinates of point#A# :
#d= 4z - 4x => d = 4*3 - 4*1 = 8# So, the cartesian equation of the plane is
#4x-4z+8=0# . -
If a plane passes through the point
#(x_0,y_0,z_0)# and has the normal vector#(a,b,c)# , then an equation of the place can be written as:#a(x-x_0)+b(y-y_0)+c(z-z_0)=0# I hope that this was helpful.