10.00 mL of a weak base was titrated with 0.215 M HCl. When the titration is halfway to equivalence, 14.96 mL of HCl has been added and the pH is 10.18. What is the initial molarity of the weak base? What is the pH at equivalence?

1 Answer
Michael
Mar 9, 2017

#sf((a))#

#sf([B]=0.643color(white)(x)"mol/l")#

#sf((b))#

#sf(pH=5.48)#

Explanation:

#sf((a))#

We will call the base B.

It gets neutralised:

#sf(B+HClrarrBH^(+)+Cl^(-))#

#sf(n_(HCl)=cxxv=0.215xx(29.92)/(1000)=6.433xx10^(-3))#

From the equation we can see that the number of moles of B must be the same:

#sf(n_B=6.433xx10^(-3))#

#sf(c=n/v)#

#:.##sf([B]=(6.433xxcancel(10^(-3)))/(10.00xxcancel(10^(-3)))=0.6433color(white)(x)"mol/l")#

#sf((b))#

The titration curve looks like this:

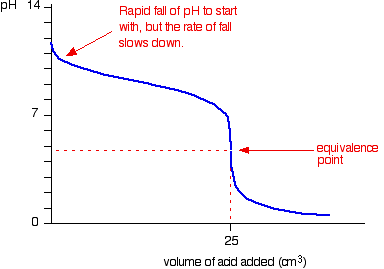
chemguide.co.uk

(our equivalence point is different)

The #sf(BH^+)# ions that form are slightly acidic:

#sf(BH^(+)rightleftharpoonsB+H^(+))#

For which:

#sf(K_a=([B][H^(+)])/([BH^+]))#

When the titration is at halfway to equivalence point we can say that:

#sf([B]=[BH^+])#

#:.##sf(K_a=(cancel([B])[H^(+)])/(cancel([BH^+])))#

#:.##sf(K_a=[H^+])#

#:.##sf(pK_a=pH=10.18)#

This is a common method of finding the #sf(pK_a)# of a weak acid.

At the equivalence point we now have a solution of #sf(BH_((aq))^+)#

We can find its pH if we know the concentration:

The volume of acid added at the equivalence point = 2 x 14.96 = 29.92 ml. This means the total volume of the solution = 29.92 + 10 = 39.92 ml.

#sf([BH^+]=n/v=(6.433xxcancel(10^(-3)))/(39.92xxcancel(10^(-3)))=0.1611color(white)(x)"mol/l")#

Since we have a weak acid we can derive this expression from an ICE table:

#sf(pH=1/2[pK_a-loga])#

Where a is the concentration of the acid which we assume to be a close approximation of the equilibrium concentration.

#:.##sf(pH=1/2[10.18-log(0.611)])#

#sf(pH=1/2[10.18+0.792])#

#sf(pH=5.48)#

This shows that the pH is slightly acidic at the equivalence point - the graph also shows this.

You would expect this result as the pH of a salt formed from a weak base and a strong acid will be slightly acidic.

This is known as "salt hydrolysis".

Related questions
See all questions in Titration Calculations
Impact of this question
11698 views around the world
You can reuse this answer
Creative Commons License