Question

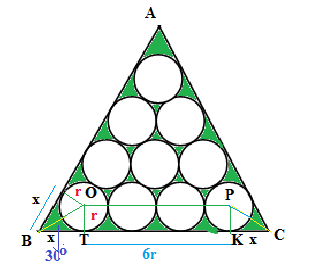
10 circular pieces of paper each of radius 1 cm have been cut out from a piece of paper having a shape of an equilateral triangle. What should be the minimum area of the equilateral triangle?

Answer 1

`A = 6(3+2sqrt(3))`[`"cm"^2`]

Explanation:

The circular pieces of paper aligned in rows, like

1 over
2 over
3 over
4

configure the skeleton of an equilateral triangle.

The external equilateral triangle must have a minimum side length of `6r` plus an addition of

`2 xx r/(tan(30^@)) = 2xx sqrt(3)xx r`.

So each side must have a length of `l=(6+2 xx sqrt(3))xxr` or `l = lambda r`. For the equilateral triangle the height is `h = sqrt(3)/2 l` so the area is given by

`A = 1/2 l xx h = 1/2 sqrt(3)/2 (lambda r)^2 = 6(3+2sqrt(3))r^2`

now if `r = 1`[`"cm"`] then `A = 6(3+2sqrt(3))`[`"cm"^2`]

Answer 2

`=6(3+2sqrt3)cm^2`

Explanation:

After cutting out 10 circular pieces the triangular paper will have structure as shown below

`r =1 cm->"Radius of each circular piece of paper"`

`BT = "projection of BO"=x`

`/_OBT=1/2/_ABC=1/2xx60^@=30^@`

`x/r=cot30^@=sqrt3`

`=>x=sqrt3r`

`"Each side of the " DeltaABC=6r+2x=6r+2sqrt3r =(6+2sqrt3) cm`

`"Area " Delta ABC=sqrt3/4*"side"^2=sqrt3/4(6+2sqrt3)^2 cm^2`

`=sqrt3(3+sqrt3)^2cm^2`

`=sqrt3(12+6sqrt3)cm^2`

`=(18+12sqrt3)cm^2`

`=6(3+2sqrt3)cm^2`