The compressibility factor is the ratio of the molar volume of a gas - the volume occupied by #1# mole of a gas at certain temperature and pressure - and to the molar volume of an ideal gas, at the same temperature and pressure. The compressibility factor (#Z#) is defined as
#Z = V_(molar)/(V_(molar(idealgas))) = (PV_(molar))/(RT)#, where
#V_(molar(idealgas)) = (RT)/P# is the molar volume of the correspondig ideal gas, #P# is the pressure, #T# is the temperature, and #R# is the ideal gas constant.
Now, the ideal gas law can be used for all gases under normal conditions; however, under more extreme conditions, real gases deviate from the ideal behavior. These deviations can be measured by
#Z = (PV)/(nRT)#; for an ideal gas, #Z# = 1; positive deviations from ideal gas behavior would have #Z >1#, while negative ones will have #Z<1#.
The van der Waals equation makes an attempt at modeling real gas behaviour starting from the ideal gas law. It makes two assumptions: molecules will now have a volume of b # L*(mol)^(-1)#, and van der Waals forces will now exist between molecules.
These will lead to a decrease in volume expressed by #V_(real) = V_(measured) - nb#, and a decrease in pressure (due to the fact that the number of collisions between molecules and the walls of the container will decrease, since now moleculs are attracted or repelled by eachother) expressed by #P = P_(ideal) - a(n/V)^2#.
Rearranging the ideal law equation with #V_(real)# and #P_(ideal)#, we get the van der Waals equation for real gases
#(P+ a(n/v)^2)(V-nb) = nRT#, where
#(P + a(n/V)^2)# - pressure correction - compensates for a smaller measured pressure by adding a term to the ideal model pressure;
#(V-nb)# - volume correction;
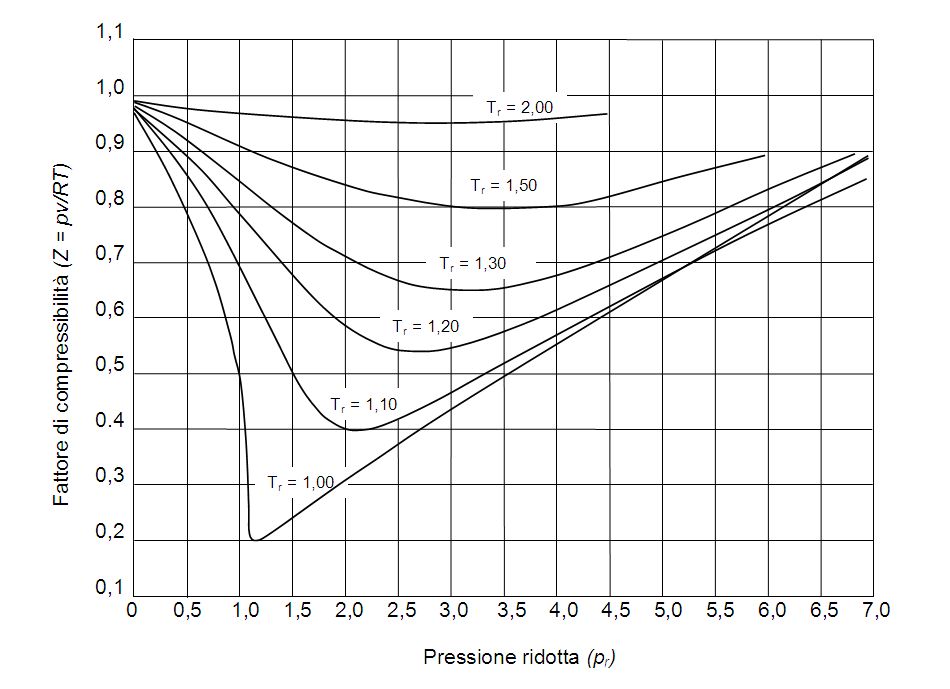
So, #Z# values are usually obtained from generalized compressibility charts such as this one: