Question #53f3b

Question

Question #53f3b

1 Answer

Impact of this question

5352 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2015-01-05T10:06:21

Since most solids have periodic arrays of atoms that form crystal lattices, which must imply a degree of symmetry in the arrangement of these lattices.

An ideal crystal can be considered to be a repetition of identical structures in 3D space. Lattices are mathematical points set at specific coordonates in space that can describe the periodicity of such a repetitive structure. Atoms, which are placed in specific lattice points, represent the identical structural units.

All possible lattices can be described by a set of three linearly independent vectors, ${\to a}_{1}$ $veca_1$ , ${\to a}_{2}$ $veca_2$ , and ${\to a}_{3}$ $veca_3$ - these represent the unit vectors of the lattice.

Every lattice point can be described by a translation of a vector $\to R$ $vecR$ described by

$\to R = n_{1} \cdot {\to a}_{1} + n_{2} \cdot {\to a}_{2} + n_{3} \cdot {\to a}_{3}$ $vecR = n_1 * veca_1 + n_2 * veca_2 + n_3 * veca_3$ ,

where $n_{1}$ $n_1$ , $n_{2}$ $n_2$ , and $n_{3}$ $n_3$ are integers.

So, a Bravais lattice represents an infinite array of discrete points that have an arrangement and an orientation that appear exactly the same from whichever point the array is viewed.

14 Bravais lattices are commonly used to classify lattice structures according to basic symmetry groups.

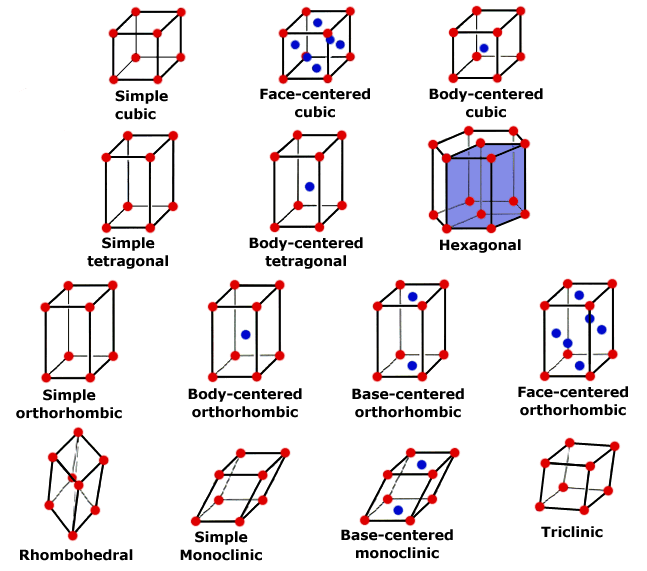http://www.seas.upenn.edu/~chem101/sschem/solidstatechem.html

Each Bravais lattice is obtained by a specific $\to R$ $vecR$ . For example, simple cubic is obtained when $a_{1} = a_{2} = a_{3}$ $a_1 = a_2 = a_3$ and the angles between the three vectors are all equal to $90^{\circ}$ $90^@$ , as you can see here:

http://www.seas.upenn.edu/~chem101/sschem/solidstatechem.html

(Here $a$ $a$ , $b$ $b$ , and $c$ $c$ were used instead of $a_{1}$ $a_1$ , $a_{2}$ $a_2$ , and $a_{3}$ $a_3$ ; $α$ $alpha$ , $β$ $beta$ , and $γ$ $gamma$ represent the angles between the three unit vectors).

Here's a video showing all the 14 Bravais lattice structures:

Science

Math

Humanities

... and beyond

Question #53f3b

1 Answer

Related questions

Impact of this question