Question #2849f
1 Answer
Use the ideal gas law equation, PV=nRT, to solve for the number of moles of oxygen produced.
Explanation:
The mass of oxygen collected over the water is
You don't need the actual equation for the decomposition reaction of
Now, here's what you're working with
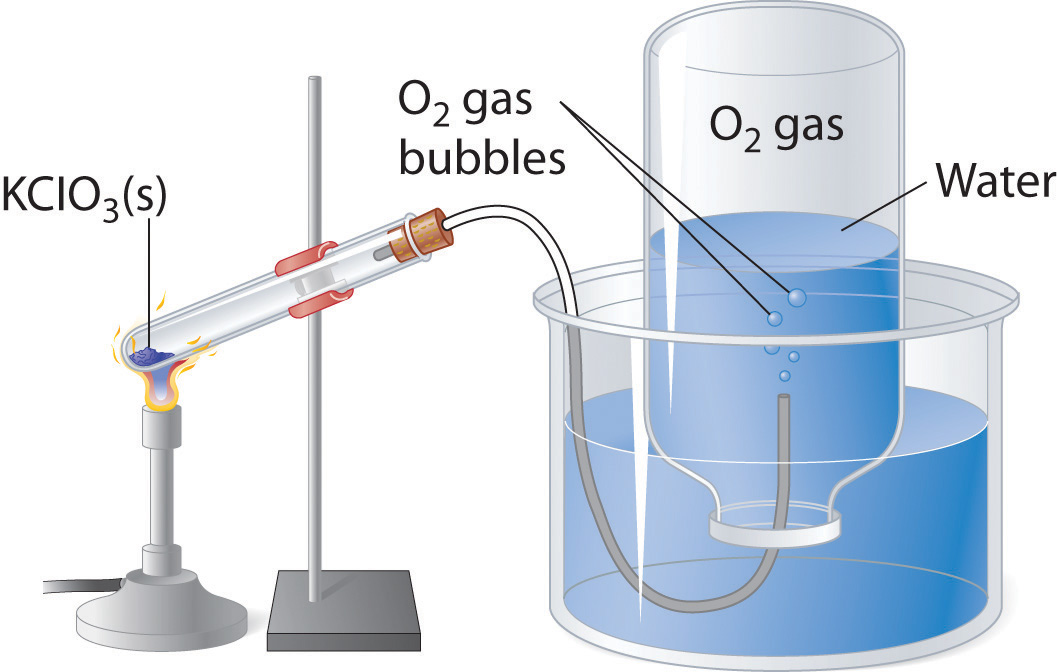
The most important thing to notice here is that the pressure at which the gas is collected includes the water vapor as well, so in order to get the proper pressure for the oxygen you must eliminate the water vapor
In your case,
Now all you have to do is use the ideal gas law equation,
I've converted all the units into those required for R = 0.082 - pressure into atm, volume into L, and temperature into K. Don't forget to do this!
Since you know how many moles of oxygen were produced, you can use oxygen's molar mass to determine the mass

