How many electrons have...?
#a)# #n = 4# , #l = 2#
#b)# #n = 4# , #l = 2# , #m_l = +2#
#c)# #n = 4# , #l = 2# , #m_l = +2# , #m_s = +1/2#
1 Answer
The answers would be a) 10 electrons, b) 2 electrons, and c) 1 electron.
I assume you're familiar with quantum numbers, so I won't go into too much detail about them.
So, here are the four quantum numbers you have to work with
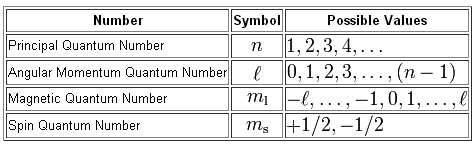
Let's start with point a). Since you already know that n = 4 and l = 2, you only have to decide the possible values for the magentic quantum number,
Since the magnetic quantum number can only go from
#m_l = -2, -1, 0, +1, +2#
SInce each of these orbitals can hold a maximum of two electrons, one having spin-up and one having spin-down, a total of 10 electrons can share the quantum numbers n = 4 and l = 2
#m_l = -2 => m_s = +- 1/2#
#m_l = -1 => m_s = +- 1/2#
#m_l = 0 => m_s = +- 1/2#
#m_l = +1 => m_s = +- 1/2#
#m_l = +2 => m_s = +- 1/2#
On to point b). Now you know that n = 4, l = 2, and
#m_s = +- 1/2#
FInally, point c). Because every electron has a specific set of quantum numbers that describes its position around the nucleus, the values given to you for all the four quantum numbers can only describe 1 electron.

