Quantum Numbers
Key Questions
-
Quantum numbers refer to electrons, so I'll assume you mean the electron number that would correspond with the atomic number of the element. Quantum numbers are basically like an address for electrons, giving us information about the location of an electron from most general to most specific.
We need to apply the Aufbau principle, Hund's rule and the Pauli exclusion principle to answer this question.
Quantum numbers are listed in the following order: n, l,
ml ,ms n = principal number - tells us which energy level an electron is in
l = angular number - tells us which sublevel and electron is in
ml = magnetic number - tells us which orbital the e- is in
ms = spin number - tells us if the electron is spin up or spin downThe quantum numbers for electron 1 (hydrogen) are: 1,0,0,+1/2
2 (He): 1,0,0,-1/2
3 (Li): 2,0,0,+1/2
4 (Be): 2,0,0,-1/2There is a lot of info you'll need to understand... - I'll recommend this video to help. Quantum numbers are discussed in the final minute but there is info through the entire video you'll use to determine quantum numbers.
-
Zero electrons.
Electrons don't share all four identical quantum numbers. Each electron has its own set of four quantum numbers. Something similar like people have unique fingerprint. Quantum number "is telling" us everything about electron.
-
Answer:
Quantum numbers can be used to describe the quantum state of an electron.
Explanation:
Quantum numbers can be used to describe the quantum state of an electron.
There are four quantum numbers for atoms:
-
n=1,2,3,... - principal quantum number; describes the energy level. -
l=0,1,2,...,n−1 - angular momentum quantum number; describes the shape of the orbital.
0↔s,1↔p,2↔d,3↔f,... , etc. The ordering iss,p,d,f,g,h,i,k,... . -
ml={−l,−l+1,...,0,...,l−1,l} - magnetic quantum number; corresponds to each unique orbital in the sublevel specified byl , and there are2l+1 such values. ms=±12 - spin quantum number; describes the spin (up/down)
A given orbital is labeled as an
nl orbital: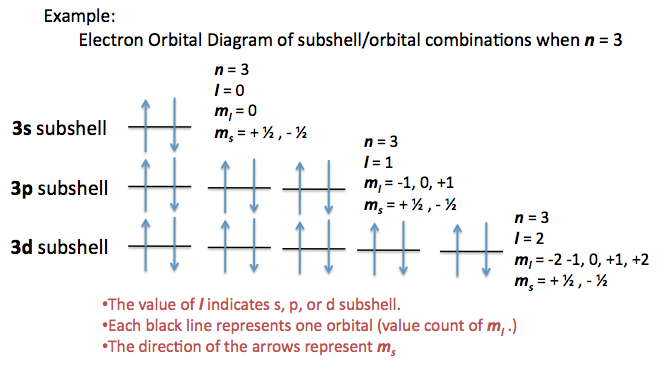
-