Question #6c02a
1 Answer
The new volume wil be
Since you gave no units for volume, I"ll use liters, but you you can use whatever units are actually given to you.
So, no mention of pressure and number of moles is made, which is an alternative way of saying they're kept constant. When this is the case, you can apply Charles' law to solve for the volume you need.
According to Charles' law, when pressure and number of moles are kept constant, the volume of an ideal gas is directly proportional to its temperature.
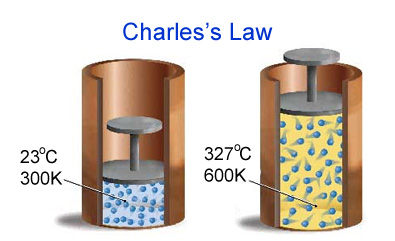
The higher the temperature, the bigger the volume the gas will occupy. Mathematically, this is expressed as
In your case, the temperature increases from
Therefore,
SIDE NOTE Do not forget to transform degrees Celsius to Kelvin, or else your result will be way off.
Also, keep an eye out for significant figures; in this case, rounding the answer to the correct number of sig figs, which is one, would make the volume smaller than the one you started with.
This is, of course, wrong, so I suspect that your temperatures should have actually been 20.0 and 35.0 degrees Celsius.

