Question

Question #20be5

Answer 1

The latent heat of vaporization of ammonia is `1 * 10^(3)"J/g"`.

The latent heat of vaporization represents the energy you must supply, in the form of heat, to a substance to change it from liquid to vapor.

You're basically dealing with a phase change, during which you supply heat to the liquid ammonia to transform it to steam - at constant temperature.

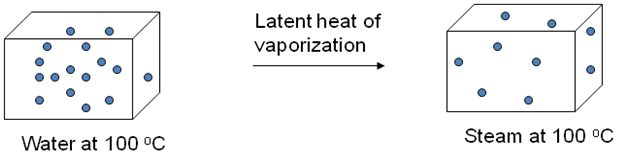
Mathematically, the amount of heat required to vaporize a certain mass of a substance is given by

`q = m * DeltaH_("vap")`, where

`q` - the heat supplied;
`m` - the mass of the substance;
`DeltaH_("vap")` - the latent heat of vaporization.

Plug in your data and solve for `DeltaH_("vap")` by

`DeltaH_("vap") = q/m = (6.5 * 10^(6)"J")/(5 * 10^(3)"g") = 1.3 * 10^(3)"J/g"`

If you round this to one sig fig, the number of sig figs given for 5 kg, the answer will be

`DeltaH_("vap") = color(green)(1 * 10^(3) "J/g")`

Answer 2

`6.5/5 = 1.3 MJ kg^-1`

Explanation:

The "Latent heat of vaporization" for a substance(in this case `NH_3`) is the heat that is required to cause a change in phase of a given mass(not specified)

We are told that `6.5 MJ` caused this change at the boiling point. Which tells that ALL the heat gained = the heat needed to change in phase.
Hence, `6.5 MJ` IS the latent heat for vaporization of `NH_3`

But the question asks for "specific" latent heat,
so we divide by the mass,
`(6.5MJ)/(5kg) = 1.3 MJ kg^-1`