This is a titration of sulfurous acid, #H_2SO_3#, a weak diprotic acid, with sodium hydroxide, #NaOH#, a strong base.
Since sulfurous acid is a diprotic acid, you'll have two equilibria reactions ,each with its own acid dissociation constant and #pK_a#
#H_2SO_(3(aq)) + H_2O_((l)) rightleftharpoons H_3O_((aq))^(+) + HSO_(3(aq))^(-)#, #pK_(a1) = 1.85#
#HSO_(3(aq))^(-) + H_2O_((l)) rightleftharpoons H_3O_((aq))^(+) + SO_(3(aq))^(2-)#, #pK_(a2) = 7.19#
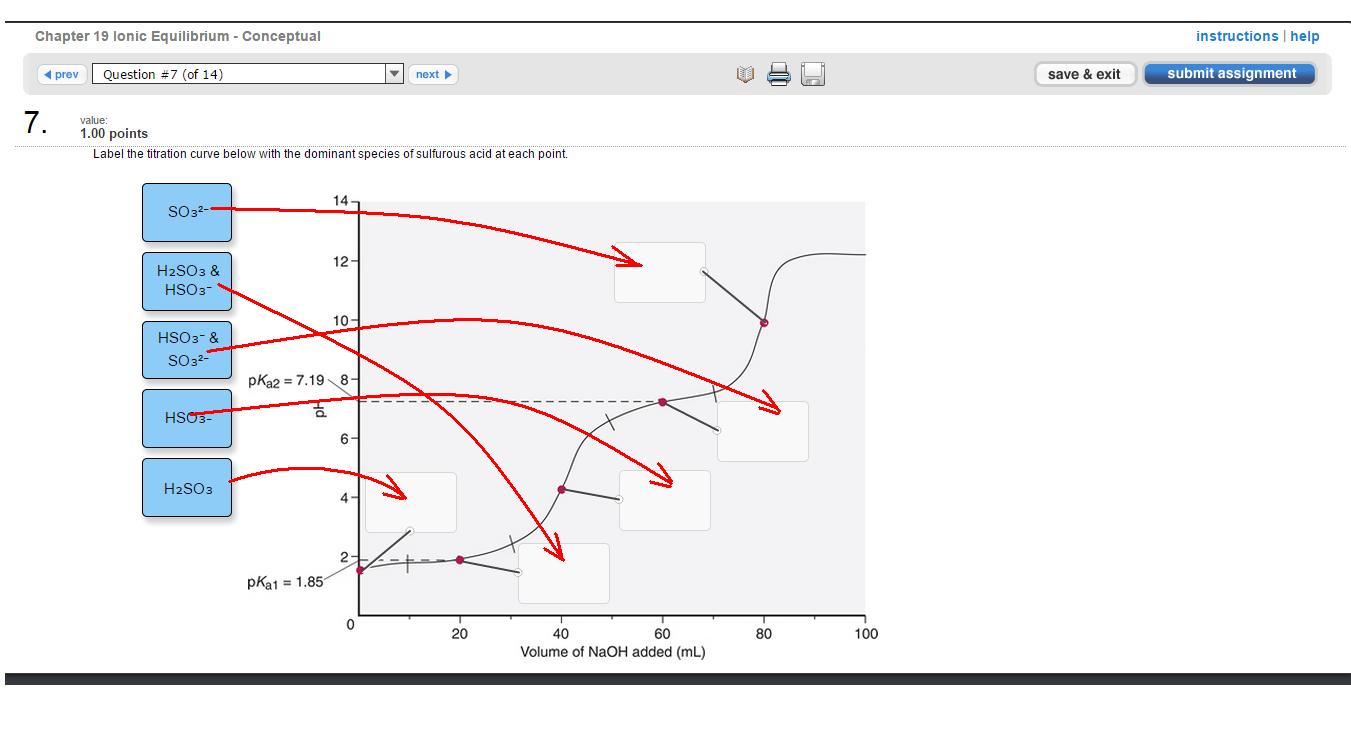
So, starting from the lower-left corner. The first point is where pH is equal to #pK_(a1)#, no base has been added, so just the #H_2SO_3# form of the acid will be in solution.
Now you start adding the base. This will increase the pH enough to trigger the buffer region at which #[H_2SO_3] = [HSO_3^(-)]#.
The next step is the first equivalence point at which the first #H^(+)# is completely dissociated from #H_2SO_3# #-># now only #HSO_3^(-)# remains in solution.
Adding more base will trigger another buffer region in which #[HSO_3^(-)] = [SO_3^(2-)]#. Notice that the pH of the solution is equal to #pK_(a2)# (think Henderson-Hasselbalch equation).
Finally, adding more base will result in a second equivalence point at which all the #H^(+)#s have been dissociated from #HSO_3^(-)#, leaving only #SO_3^(2-)# in solution.

