Question #09585
1 Answer
The solution in which you dissolve the sodium chloride will have a lower freezing point.
This happens because freezing-point depression is a colligative property that depends on the concentration of particles in solution, not on what those particles are.
Mathematically, this is expressed as
The van't Hoff factor is the key to why the sodium chloride solution will have a lower freezing point.
Sodium chloride is a strong electrolyte, which means it dissociates completely in aqueous solution to give sodium cations and chloride anions
Notice that 1 mole of
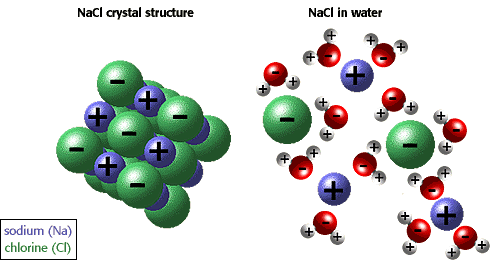
As a result, the van't Hoff factor for
This is not the case for ethanol. When placed in aqueous solution, a non-electrolyte does not dissociate to form ions. As a result, its van't Hoff factor will be equal to 1.
To compare the freezing points of the two solutions, just use
or
As you can see,

