Question #06e3e
1 Answer
The tetrathionate anion,
Here's how that happens. If you assign oxidation numbers to each atom that takes part in the reaction, you'll get
Notice that sulfur has a fractional oxidation number of +2.5. What that means is that not all the sulfur atoms present in the tetrathionate molecule have the same oxidation number.
In fact, +2.5 is the average of those oxidation numbers. Here's why that is
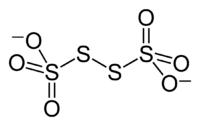
The two sulfur atoms that are bonded to each other have an oxidation number of zero. At the same time, the two sulfur atoms that are each bonded to 3 oxygen atoms will have an oxidation number of +5.
The average oxidation number of the sulfur atoms in the tetrathionate molecule will thus be
So, on the reactants' side you have 4 sulfur atoms,
You go from a total of +10 to a total of +8 by losing two electrons
The net charge is equal on both sides.

