The maximum number of electrons that can have those two values for n and m_l is 4.
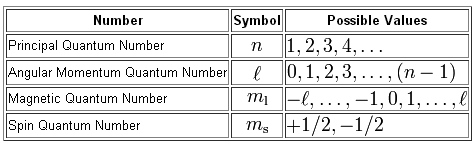
You are given the values for n, the principal quantum number, and m_l, the magnetic quantum number, so you must first determine how many orbitals can have these two values for their respective quantum numbers, then determine how many electrons can each of those orbitals hold.
 )
)
The value of m_l depends on the value of l, the angular momentum quantum number, which in turn depends on the value of n.
For n = 4, only two values for l can allow m_l to take the value 2, l = 2 and l = 3.
This means that you get two orbitals that match those two quantum numbers
n=4; l=2; m_l ="+2" -> a 4d-orbital;
n=4; l=3; m_l = "+2" -> a 4f-orbital;
Since each of the two orbitals can hold a maximum of two electrons, the maximum number of electrons that have those two quantum numbers will be 4
n = 4; l = 2; m_l = "+2"; m_s = "+1/2"
n = 4; l = 2; m_l ="+2"; m_s = "-1/2"
n = 4; l = 3; m_l = "+2"; m_s = "+1/2"
n = 4; l = 3; m_l = "+2"; m_s = "-1/2"
 )
) 

