Question #fcdef
1 Answer
The net force on level ground is 200 N, and the net force on an incline plane at a
On Level Ground
Calculate the acceleration using the equation
The net force causes acceleration. The net force is the vector sum of all of the forces acting on a body. In this case, the weight of the object is equal to but opposite the normal force. So they are balanced and their sum is
The applied force and frictional force will determine the net force. Since no information about friction has been given, we can infer that the vector sum of the applied force and the frictional force is the net force.
Frictionless Inclined Plane
Note: Because of the nature of an inclined plane, we will use the mass of the object, but not the acceleration used for level ground. Instead we will be using the acceleration due to gravity,
We first need to determine the net force.
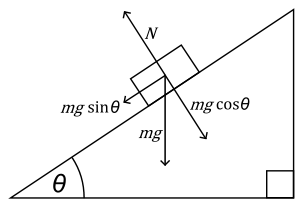 http://en.wikipedia.org/wiki/Frictionless_plane
http://en.wikipedia.org/wiki/Frictionless_plane
Weight =
Determine the weight,
The net force is equal to the parallel force vector.
Let's go ahead and determine the acceleration of the object. As stated before, on an inclined plane,
Sources:
http://www.physicsclassroom.com/class/vectors/Lesson-3/Inclined-Planes
http://en.wikipedia.org/wiki/Frictionless_plane

