Question

A parabola `y=x^2` is parametrised by `x=t` and `y=t^2`. A point P lies on the normal to the parabola at `A(t,t^2)`, and AP is 1 unit in length. Find the equation of the loci of the point `P` as `A` moves?

Answer 1

`P = P(t -2tsqrt(1/(4t^2+1)), t^2 +sqrt(1/(4t^2+1)))`

So the parametric equations of P are:

`P_x(t) = t -2tsqrt(1/(4t^2+1))`
`p_y(t) = t^2 +sqrt(1/(4t^2+1))`

Explanation:

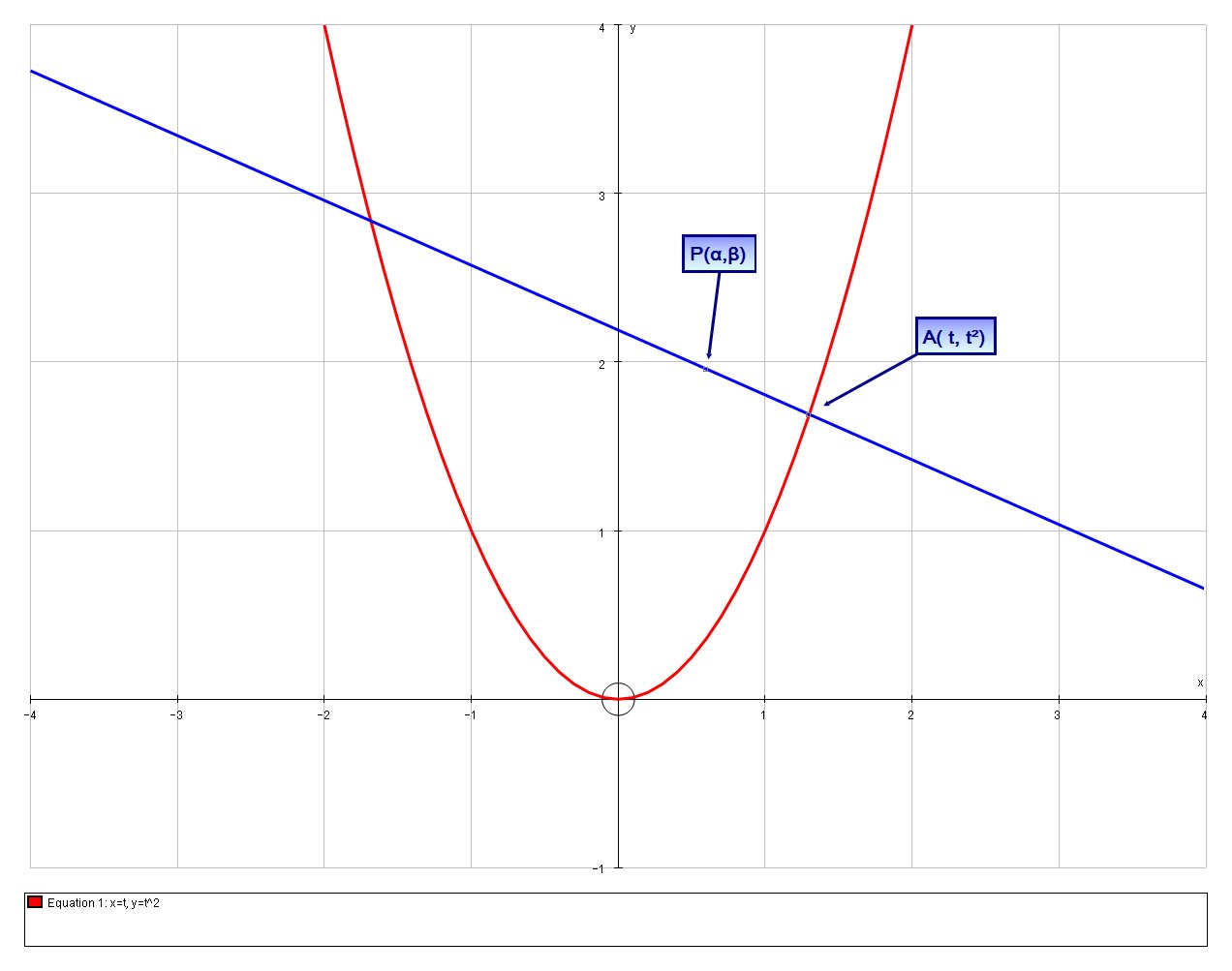
Our parabola `y=x^2` is parametrised by `x=t` and `y=t^2`, and `A(t,t^2)` is a general point on the parabola, and we give the point `P` the coordinates (to be determined) `P(alpha, beta)`

Differentiating wrt `x` we have:

`dy/dx=2x = 2t`

So the gradient of the tangent at `A` is given by `dy/dx=t`, We are told that `AP` is perpendicular to to parabola, in other words, it is perpendicular to the tangent at A. Hence the gradient of AP is `-1/(2t)` as the product of their gradients are -1.

We can now form the equation of the normal `AP` using the point-slope form of the straight line, `y-y_1=m(x-x_1)`:

`y-t^2=-1/(2t)(x-t)`
`:. 2ty-2t^3=-(x-t)`
`:. 2ty-2t^3=+t-x`

`P(alpha, beta)` lies on this line, giving:

`:. 2tbeta-2t^3 = t -alpha`

And we are also told that `AP` has length 1, so by Pythagoras:

`(t-alpha)^2+(t^2-beta)^2=1^2`

We can combine these equations to eliminate `t -alpha`:

`(2tbeta-2t^3)^2+(t^2-beta)^2=1`
`:. 4t^2beta^2-8t^4beta+4t^6 + t^4-2t^2beta+beta^2 = 1`
`:. (4t^2+1)beta^2-2t^2(4t^2+1)beta +t^4(4t^2+1)=1`
`:. beta^2-2t^2beta +t^4=1/(4t^2+1)`
`:. beta^2-2t^2beta +t^4-1/(4t^2+1) =0`

We can solve this quadratic in `beta` by completing the square to get:

`(beta-t^2)^2-t^4 +t^4-1/(4t^2+1) =0`
`:. (beta-t^2)^2 = 1/(4t^2+1)`
`:. beta-t^2 = +-sqrt(1/(4t^2+1))`
`:. beta = t^2 +-sqrt(1/(4t^2+1))`

We have found two solutions because there is one point `AP` distance `1` unit extending inwards,and one point extending outwards. Intuitively we choose `beta=t^2 +sqrt(1/(4t^2+1))`.

Now from before we have:

`2tbeta-2t^3 = t -alpha` :
`:. alpha = t -2tbeta+2t^3`

Substituting our valu of `beta`, from above, gives us:

`alpha = t -2t(t^2 +sqrt(1/(4t^2+1)))+2t^3`
`alpha = t -2t^3 -2tsqrt(1/(4t^2+1))+2t^3`
`alpha = t -2tsqrt(1/(4t^2+1))`

And so the general coordinates of `P(alpha,beta)` in term of `t` are:

`P = P(t -2tsqrt(1/(4t^2+1)), t^2 +sqrt(1/(4t^2+1)))`

So the parametric equations of P are:

`P_x(t) = t -2tsqrt(1/(4t^2+1))`
`p_y(t) = t^2 +sqrt(1/(4t^2+1))`

The loci traced out by `P` as `A` moves along the parabola is shown in the following graph in green:

Answer 2

`((x_p=t-(2t)/sqrt(4t^2+1)),(y_p=t^2+1/sqrt(4t^2+1)))`

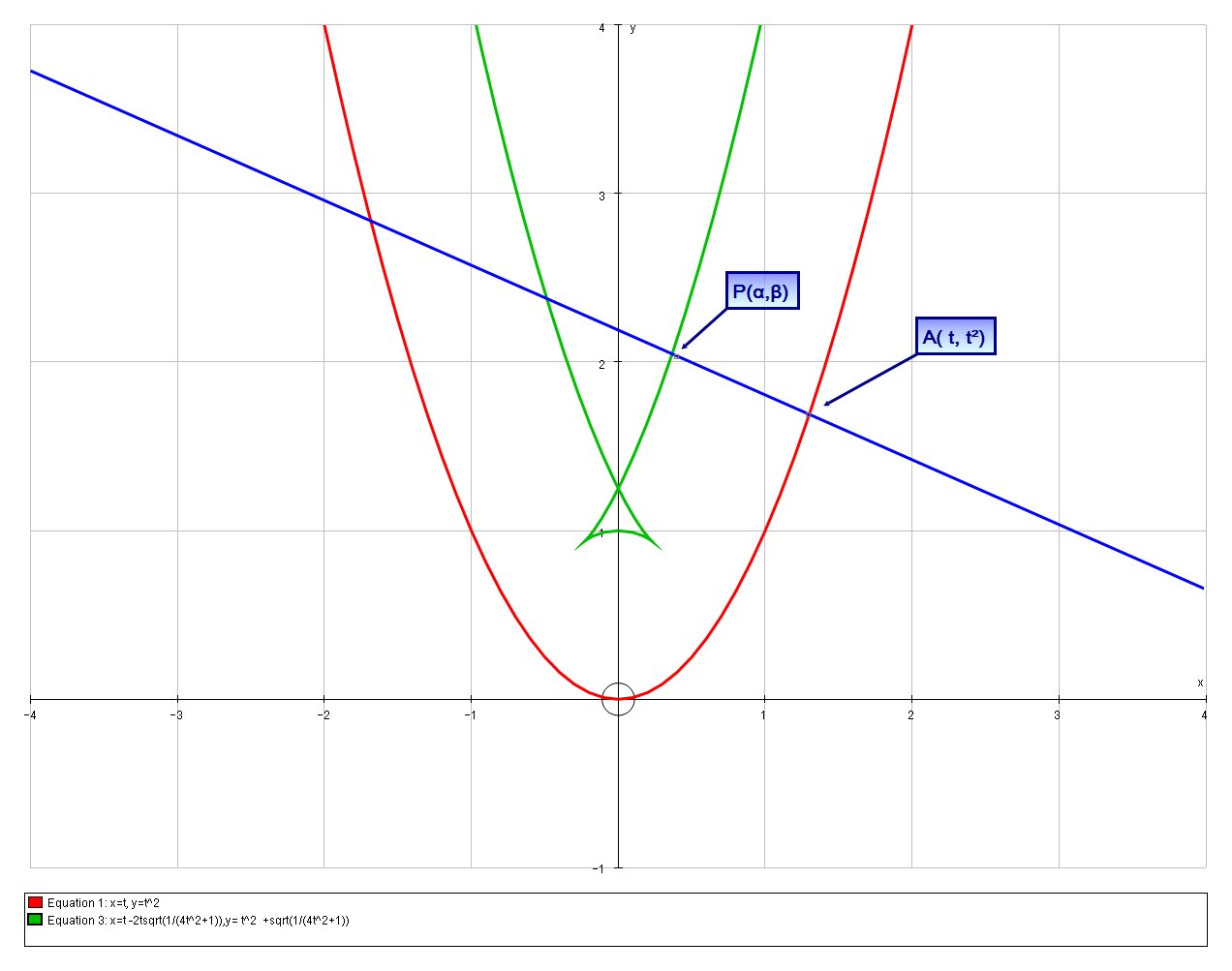
Explanation:

Given `f(x,y)=y-x^2=0` the normal vector at point `(x_0,f(x_0))` is obtained as `\vec n = ((partial f)/(partial x), (partial f)/(partial y))=(-2x,1)`

but `(x,y)=(t,t^2)`. The point coordinates of the sought geometric place is given by

`p=(x,y)+d (vec n)/norm(vec n)` or

`p = (t,t^2)+d{(-2t,1)}/sqrt((-2t)^2+1)` or

`((x_p=t-2d(t/sqrt(4t^2+1))),(y_p=t^2+d/sqrt(4t^2+1)))`, Now if `d=1`

`((x_p=t-(2t)/sqrt(4t^2+1)),(y_p=t^2+1/sqrt(4t^2+1)))`