Question #b0e61
1 Answer
The titration curve tells us the volume of titrant necessary to completely neutralise a solution.
Explanation:
Titration is a very important experiment done in laboratory. Imagine this situation: a rookie student left in the lab a flask, let's say a beaker, containing hydrochloric acid (
He was a little sloppy and totally forgot to take notes, so its concentration is unknown . You, being a rightly curious scientist, want to find out the solution's concentration.
Because your lab is very well-equipped, you readily find some strong base, for example sodium hydroxide (
You clean up your lab, get the appropriate equipment and start the experiment known as titration . This is the basic setup:
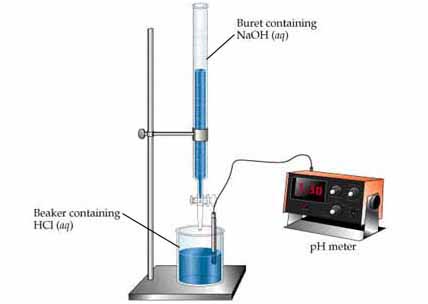
Very carefully, you open the valve (known as a stopcock) in the burette and the base (the titrant in this case) slowly begins to drop (no pun intended).
You can have a pH meter analysing the solution's pH in real-time, if you want. The solution in the beaker must be stirred throughout the entire experiment.
Eventually, the solution in the beaker will start to turn pink, because of the phenolphthalein . Kind of slowly at first - stir, then it's colourless again. However, at some point it will turn completely pink. Very light pink, just enough that it's not entirely colourless any more.
That's when you know you've reached the equivalence point.
The equivalence point happens when all of the acid or base in the solution has been neutralised by the titrant. If you've been measuring the pH and plotting a graph, you will end up with something like this:
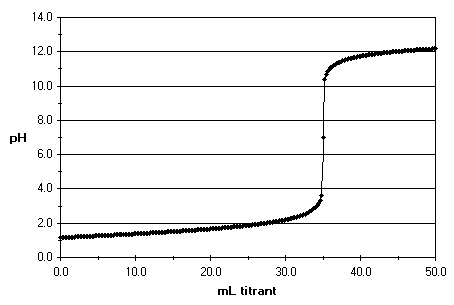
When the solution has been completely neutralised, its pH is 7. The pH is a scale that shows the concentration of
pH is, mathematically,
So in this case we are adding
By looking at the y-axis in the graph and finding the point where the pH is equal to seven , you can find out how much titrant was used by then. Now, the only step remaining is doing the maths: stoichiometry time!
You know the concentration of the titrant and its volume, and you also know the volume of the solution being analysed; work out how many moles of titrant reacted with all of the acid or base, then how many moles of acid or base there were in the solution to begin with, and finally calculate its concentration in moles per litre.
Hope this helped :^).


