Question

Question #2c334

Answer 1

Its new volume will be equal to 3 L.

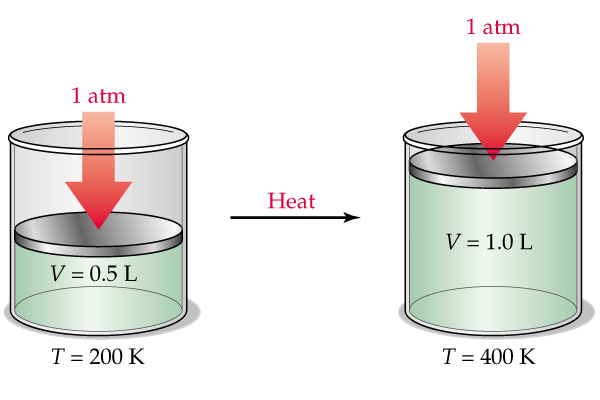
You know that pressure and number of moles are kept constnt, which means that you can use Charles' Law to determine what volume your gas will occupy at that new temperature.

According to Charles' Law, the volume and temperature of a gas have a direct relationship when pressure and number of moles are kept constant.

In other words, when temperature increases, volume increases, and when temperature decreases, volume decreases as well.

Mathematically, this is expressed as

`V_1/T_1 = V_2/T_2`, where

`V_1`, `T_1` - the volume and temperature at an initial state;
`V_2`, `T_2` - the volume and temperature at a final state.

Plug your values into the above equation and solve for `V_2`

`V_2 = T_2/T_1 * V_1`

`V_2 = ((273.15 + 25)cancel("K"))/((273.15 + 300)cancel("K")) * "6.55 L" = "3.407 L"`

Since you only gave one sig fig for the first temperature of the gas, the answer must be rounded to one sig fig

`V_2 = color(green)("3 L")`

SIDE NOTE Do not forget to convert the temperature from degrees Celsius to Kelvin!